��Ŀ����
����Ŀ����ͼ��ʾ��AB����Ǧ�Ϊ45���ֱ�����CD�ǰ뾶R=0.4m��Բ�����������ͨ��һ������BCƽ����ӣ��������������ֱƽ�����Ҵ����⻬��һ������m=1kg�����壨���Կ����ʵ㣩�Ӹ�H�ĵط��ɾ�ֹ�ͷţ��������Բ����ߵ�D��ɳ�����ֱб�����P�㣮��֪P����Բ����Բ��O�ȸߣ�gȡ10m/s2 �� ��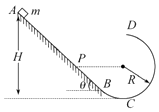
��1���������P��ǰ˲����ٶȣ�
��2����C�����������ѹ����С��
��3�����徲ֹ�ͷ�ʱ�ĸ߶�H��
���𰸡�
��1���⣺�����D���˶���P����ƽ���˶�����ֱ���������������˶�������ֱ�����У�
2gR=vy2��
��ã�vy= ![]() =
= ![]() =2
=2 ![]() m/s
m/s
���ݼ��ι�ϵ�ã��������P����ٶ� vP= ![]() =4m/s
=4m/s
���������P��ǰ˲����ٶ�Ϊ4m/s
��2���⣺��C��P�Ĺ��̣����ݻ�е���غ㶨�ɵã�
mgR= ![]() ��
�� ![]()
��C�㣬��ţ�ٵڶ����ɵã�
N��mg=m ![]()
������� N=70N
����C�����������ѹ��Ϊ70N
��3���⣺�����A��P�Ĺ����У����ݻ�е���غ㶨�ɵã�
mg��H��R��= ![]() mvP2��
mvP2��
��ã�H=1.2m
�����徲ֹ�ͷ�ʱ�ĸ߶�HΪ1.2m
����������1�������D���˶���P����ƽ���˶�����ֱ���������������˶��������ٶ�λ�ƹ�ʽ�������P��ʱ��ֱ�����ٶȣ������������P����ٶȣ���2�����ݻ�е���غ㶨�����������C����ٶȣ���C�㣬������������ʽ��ʽ������������֧��������3�������A��D�Ĺ����У����ݻ�е���غ㶨����ʽ������⣮
�����㾫�����������⣬������Ҫ�˽��е���غ㼰������(��ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ���)����Ҫ���ջ�е���ۺ�Ӧ��(ϵͳ��̬���ܻ�е��E 1 ����ĩ̬���ܻ�е��E 2 ����E1 =E2��ϵͳ���ٵ����������ܦ�E P�� ����ϵͳ���ӵ��ܶ��ܦ�E K�� ������E P�� =��E K������ϵͳֻ��A��

 ��У����ϵ�д�
��У����ϵ�д�