题目内容

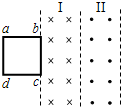精英家教网空间内有两个沿竖直方向的有界匀强磁场I、II，磁感应强度大小均为B，宽度均为L，边界线平行，磁场I竖直向下，磁场II竖直向上，如图所示为俯视图．一边长为L、质量为m的正方形导线框abcd放在光滑绝缘的水平面上，在水平恒力F作用下沿水平面通过两个磁场区域．线框的bc边始终平行于磁场区的边界，力F垂直于bc边，当bc边进入磁场I时，线框恰以速度v0做匀速运动，此时线框中的电流为i0；当ad边将要离开磁场II时线框中的电流稍小于i0，则（　　）
分析：bc边在磁场II中运动时，ad和bc两边都切割磁感线，产生感应电动势，根据右手定则判断感应电流的方向；根据E=BLv、I=
E
R
和安培力公式F=BIL，得到安培力与速度的表达式，由牛顿第二定律求出加速度；
bc边恰离开磁场II时，做加速度减小的减速运动，将该过程与匀减速运动的时间比较，分析离开磁场II时的速度大小；
根据bc离开磁场的速度分析，bc边在磁场II中运动的过程中线框中电流的最小值．
解答：解：A、bc边在磁场II中运动时，ad和bc两边都切割磁感线，根据右手定则判断得知线框中感应电流方向为abcda．故A错误．
B、bc边恰进入磁场II时线框中感应电动势为E=2BLv0，感应电流为i=
E
R
，安培力为FA=2BiL，得FA=
4B2L2v0
R

而bc进入磁场I的过程中，有F=
B2L2v0
R
．则得FA=4F．根据牛顿第二定律得：FA-F=ma，解得bc边恰进入磁场II时线框的加速度大小为a=
3F
m
．故B正确．
D、ad边将要离开磁场II时线框中的电流稍小于i0，线框的速度小于v0，线框bc边恰进入磁场II时速度为v0，线框又做减速运动，所以bc边在磁场II中运动的过程中线框中电流的最小值一定小于i0．故D正确．
C、若bc边恰离开磁场II时线框的速度大小为
v0
2
．线框中产生的感应电流为i=
2BL?
v0
2
R
=i0，而bc边在磁场II中运动的过程中线框中电流的最小值一定小于i0．故C错误．
故选BD
点评：本题关键通过分析和计算得出安培力的表达式，运用牛顿第二定律和运动学公式处理，同时要掌握右手定则．
练习册系列答案
相关题目

某同学设想用带电粒子的运动轨迹做出“0”、“8”字样，首先，如图甲所示，在真空空间的竖直平面内建立直角坐标系，在和处有两个与轴平行的水平界面和，它们把空间分成Ⅰ、Ⅱ、Ⅲ三个区域，在三个区域内分别存在匀强磁场、、，其   

大小满足，方

向如图甲所示．在Ⅱ区域内的轴左右

两侧还分别存在匀强电场、(图中

未画出)，忽略所有电、磁场的边缘效应．

是以坐标原点为中心对称的正方

形，其边长．现在界面上的

A处沿轴正方向发射一比荷的带正电荷的粒子(重力不计)，粒子恰能沿图中实线途经B、C、，D三点后回到A点并做周期性运动，轨迹构成一个“0”字．已知粒子每次穿越Ⅱ区域时均做直线运动．

    (1)求、的大小和方向．

    (2)去掉Ⅱ和Ⅲ区域中的匀强电场和磁场，其他条件不变，仍在A处以相同的速度发射相同的粒子，请在Ⅱ和Ⅲ区城内重新设计适当的匀强电场或匀强磁场，使粒子运动的轨迹成为上下对称的“8”字，且粒子运动的周期跟甲图中相同．请通过必要的计算和分析，求出你所设计的“场”的大小、方向和区域，并在乙图中描绘出带电粒子的运动轨迹和你所设计的“场”．(上面半圆轨迹已在图中画出)

第六部分 振动和波

第一讲 基本知识介绍

《振动和波》的竞赛考纲和高考要求有很大的不同，必须做一些相对详细的补充。

一、简谐运动

1、简谐运动定义：= －k             ①

凡是所受合力和位移满足①式的质点，均可称之为谐振子，如弹簧振子、小角度单摆等。

谐振子的加速度：= －

2、简谐运动的方程

回避高等数学工具，我们可以将简谐运动看成匀速圆周运动在某一条直线上的投影运动（以下均看在x方向的投影），圆周运动的半径即为简谐运动的振幅A 。

依据：x = －mω2Acosθ= －mω2

对于一个给定的匀速圆周运动，m、ω是恒定不变的，可以令：

mω2 = k 

这样，以上两式就符合了简谐运动的定义式①。所以，x方向的位移、速度、加速度就是简谐运动的相关规律。从图1不难得出——

位移方程： = Acos(ωt + φ)                                        ②

速度方程： = －ωAsin(ωt +φ)                                     ③

加速度方程：= －ω2A cos(ωt +φ)                                   ④

相关名词：(ωt +φ)称相位，φ称初相。

运动学参量的相互关系：= －ω2

A = 

tgφ= －

3、简谐运动的合成

a、同方向、同频率振动合成。两个振动x1 = A1cos(ωt +φ1)和x2 = A2cos(ωt +φ2) 合成，可令合振动x = Acos(ωt +φ) ，由于x = x1 + x2 ，解得

A =  ，φ= arctg 

显然，当φ2－φ1 = 2kπ时（k = 0，±1，±2，…），合振幅A最大，当φ2－φ1 = （2k + 1）π时（k = 0，±1，±2，…），合振幅最小。

b、方向垂直、同频率振动合成。当质点同时参与两个垂直的振动x = A1cos(ωt + φ1)和y = A2cos(ωt + φ2)时，这两个振动方程事实上已经构成了质点在二维空间运动的轨迹参数方程，消去参数t后，得一般形式的轨迹方程为

+－2cos(φ2－φ1) = sin2(φ2－φ1)

显然，当φ2－φ1 = 2kπ时（k = 0，±1，±2，…），有y = x ，轨迹为直线，合运动仍为简谐运动；

当φ2－φ1 = （2k + 1）π时（k = 0，±1，±2，…），有+= 1 ，轨迹为椭圆，合运动不再是简谐运动；

当φ2－φ1取其它值，轨迹将更为复杂，称“李萨如图形”，不是简谐运动。

c、同方向、同振幅、频率相近的振动合成。令x1 = Acos(ω1t + φ)和x2 = Acos(ω2t + φ) ，由于合运动x = x1 + x2 ，得：x =（2Acost）cos（t +φ）。合运动是振动，但不是简谐运动，称为角频率为的“拍”现象。

4、简谐运动的周期

由②式得：ω=  ，而圆周运动的角速度和简谐运动的角频率是一致的，所以

T = 2π                                                      ⑤

5、简谐运动的能量

一个做简谐运动的振子的能量由动能和势能构成，即

= mv2 + kx2 = kA2

注意：振子的势能是由（回复力系数）k和（相对平衡位置位移）x决定的一个抽象的概念，而不是具体地指重力势能或弹性势能。当我们计量了振子的抽象势能后，其它的具体势能不能再做重复计量。

6、阻尼振动、受迫振动和共振

和高考要求基本相同。

二、机械波

1、波的产生和传播

产生的过程和条件；传播的性质，相关参量（决定参量的物理因素）

2、机械波的描述

a、波动图象。和振动图象的联系

b、波动方程

如果一列简谐波沿x方向传播，振源的振动方程为y = Acos（ωt + φ），波的传播速度为v ，那么在离振源x处一个振动质点的振动方程便是

y = Acos〔ωt + φ - ·2π〕= Acos〔ω（t - ）+ φ〕

这个方程展示的是一个复变函数。对任意一个时刻t ，都有一个y（x）的正弦函数，在x-y坐标下可以描绘出一个瞬时波形。所以，称y = Acos〔ω（t - ）+ φ〕为波动方程。

3、波的干涉

a、波的叠加。几列波在同一介质种传播时，能独立的维持它们的各自形态传播，在相遇的区域则遵从矢量叠加（包括位移、速度和加速度的叠加）。

b、波的干涉。两列波频率相同、相位差恒定时，在同一介质中的叠加将形成一种特殊形态：振动加强的区域和振动削弱的区域稳定分布且彼此隔开。

我们可以用波程差的方法来讨论干涉的定量规律。如图2所示，我们用S1和S2表示两个波源，P表示空间任意一点。

当振源的振动方向相同时，令振源S1的振动方程为y1 = A1cosωt ，振源S1的振动方程为y2 = A2cosωt ，则在空间P点（距S1为r1 ，距S2为r2），两振源引起的分振动分别是

y1′= A1cos〔ω（t ? ）〕

y2′= A2cos〔ω（t ? ）〕

P点便出现两个频率相同、初相不同的振动叠加问题（φ1 =  ，φ2 = ），且初相差Δφ= （r2 – r1）。根据前面已经做过的讨论，有

r2 ? r1 = kλ时（k = 0，±1，±2，…），P点振动加强，振幅为A1 + A2 ；

r2 ? r1 =（2k ? 1）时（k = 0，±1，±2，…），P点振动削弱，振幅为│A1－A2│。

4、波的反射、折射和衍射

知识点和高考要求相同。

5、多普勒效应

当波源或者接受者相对与波的传播介质运动时，接收者会发现波的频率发生变化。多普勒效应的定量讨论可以分为以下三种情况（在讨论中注意：波源的发波频率f和波相对介质的传播速度v是恒定不变的）——

a、只有接收者相对介质运动（如图3所示）

设接收者以速度v1正对静止的波源运动。

如果接收者静止在A点，他单位时间接收的波的个数为f ，

当他迎着波源运动时，设其在单位时间到达B点，则= v1 ，、

在从A运动到B的过程中，接收者事实上“提前”多接收到了n个波

n = = = 

显然，在单位时间内，接收者接收到的总的波的数目为：f + n = f ，这就是接收者发现的频率f1 。即

f1 = f 

显然，如果v1背离波源运动，只要将上式中的v1代入负值即可。如果v1的方向不是正对S ，只要将v1出正对的分量即可。

b、只有波源相对介质运动（如图4所示）

设波源以速度v2正对静止的接收者运动。

如果波源S不动，在单位时间内，接收者在A点应接收f个波，故S到A的距离：= fλ 

在单位时间内，S运动至S′，即= v2 。由于波源的运动，事实造成了S到A的f个波被压缩在了S′到A的空间里，波长将变短，新的波长

λ′= = = = 

而每个波在介质中的传播速度仍为v ，故“被压缩”的波（A接收到的波）的频率变为

f2 = = f 

当v2背离接收者，或有一定夹角的讨论，类似a情形。

c、当接收者和波源均相对传播介质运动

当接收者正对波源以速度v1（相对介质速度）运动，波源也正对接收者以速度v2（相对介质速度）运动，我们的讨论可以在b情形的过程上延续…

f3 =  f2 = f 

关于速度方向改变的问题，讨论类似a情形。

6、声波

a、乐音和噪音

b、声音的三要素：音调、响度和音品

c、声音的共鸣

第二讲 重要模型与专题

一、简谐运动的证明与周期计算

物理情形：如图5所示，将一粗细均匀、两边开口的U型管固定，其中装有一定量的水银，汞柱总长为L 。当水银受到一个初始的扰动后，开始在管中振动。忽略管壁对汞的阻力，试证明汞柱做简谐运动，并求其周期。

模型分析：对简谐运动的证明，只要以汞柱为对象，看它的回复力与位移关系是否满足定义式①，值得注意的是，回复力系指振动方向上的合力（而非整体合力）。当简谐运动被证明后，回复力系数k就有了，求周期就是顺理成章的事。

本题中，可设汞柱两端偏离平衡位置的瞬时位移为x 、水银密度为ρ、U型管横截面积为S ，则次瞬时的回复力

ΣF = ρg2xS = x

由于L、m为固定值，可令： = k ，而且ΣF与x的方向相反，故汞柱做简谐运动。

周期T = 2π= 2π

答：汞柱的周期为2π 。

学生活动：如图6所示，两个相同的柱形滚轮平行、登高、水平放置，绕各自的轴线等角速、反方向地转动，在滚轮上覆盖一块均质的木板。已知两滚轮轴线的距离为L 、滚轮与木板之间的动摩擦因素为μ、木板的质量为m ，且木板放置时，重心不在两滚轮的正中央。试证明木板做简谐运动，并求木板运动的周期。

思路提示：找平衡位置（木板重心在两滚轮中央处）→ú力矩平衡和Σ?F6= 0结合求两处弹力→ú求摩擦力合力…

答案：木板运动周期为2π 。

巩固应用：如图7所示，三根长度均为L = 2.00m地质量均匀直杆，构成一正三角形框架ABC，C点悬挂在一光滑水平轴上，整个框架可绕转轴转动。杆AB是一导轨，一电动松鼠可在导轨上运动。现观察到松鼠正在导轨上运动，而框架却静止不动，试讨论松鼠的运动是一种什么样的运动。

解说：由于框架静止不动，松鼠在竖直方向必平衡，即：松鼠所受框架支持力等于松鼠重力。设松鼠的质量为m ，即：

N = mg                            ①

再回到框架，其静止平衡必满足框架所受合力矩为零。以C点为转轴，形成力矩的只有松鼠的压力N、和松鼠可能加速的静摩擦力f ，它们合力矩为零，即：

MN = Mf

现考查松鼠在框架上的某个一般位置（如图7，设它在导轨方向上距C点为x），上式即成：

N·x = f·Lsin60°                 ②

解①②两式可得：f = x ，且f的方向水平向左。

根据牛顿第三定律，这个力就是松鼠在导轨方向上的合力。如果我们以C在导轨上的投影点为参考点，x就是松鼠的瞬时位移。再考虑到合力与位移的方向因素，松鼠的合力与位移满足关系——

= －k

其中k =  ，对于这个系统而言，k是固定不变的。

显然这就是简谐运动的定义式。

答案：松鼠做简谐运动。

评说：这是第十三届物理奥赛预赛试题，问法比较模糊。如果理解为定性求解，以上答案已经足够。但考虑到原题中还是有定量的条件，所以做进一步的定量运算也是有必要的。譬如，我们可以求出松鼠的运动周期为：T = 2π = 2π = 2.64s 。

二、典型的简谐运动

1、弹簧振子

物理情形：如图8所示，用弹性系数为k的轻质弹簧连着一个质量为m的小球，置于倾角为θ

第二部分  牛顿运动定律

第一讲 牛顿三定律

一、牛顿第一定律

1、定律。惯性的量度

2、观念意义，突破“初态困惑”

二、牛顿第二定律

1、定律

2、理解要点

a、矢量性

b、独立作用性：ΣF → a ，ΣFx → ax …

c、瞬时性。合力可突变，故加速度可突变（与之对比：速度和位移不可突变）；牛顿第二定律展示了加速度的决定式（加速度的定义式仅仅展示了加速度的“测量手段”）。

3、适用条件

a、宏观、低速

b、惯性系

对于非惯性系的定律修正——引入惯性力、参与受力分析

三、牛顿第三定律

1、定律

2、理解要点

a、同性质（但不同物体）

b、等时效（同增同减）

c、无条件（与运动状态、空间选择无关）

第二讲 牛顿定律的应用

一、牛顿第一、第二定律的应用

单独应用牛顿第一定律的物理问题比较少，一般是需要用其解决物理问题中的某一个环节。

应用要点：合力为零时，物体靠惯性维持原有运动状态；只有物体有加速度时才需要合力。有质量的物体才有惯性。a可以突变而v、s不可突变。

1、如图1所示，在马达的驱动下，皮带运输机上方的皮带以恒定的速度向右运动。现将一工件（大小不计）在皮带左端A点轻轻放下，则在此后的过程中（      ）

A、一段时间内，工件将在滑动摩擦力作用下，对地做加速运动

B、当工件的速度等于v时，它与皮带之间的摩擦力变为静摩擦力

C、当工件相对皮带静止时，它位于皮带上A点右侧的某一点

D、工件在皮带上有可能不存在与皮带相对静止的状态

解说：B选项需要用到牛顿第一定律，A、C、D选项用到牛顿第二定律。

较难突破的是A选项，在为什么不会“立即跟上皮带”的问题上，建议使用反证法（t → 0 ，a → ∞ ，则ΣFx → ∞ ，必然会出现“供不应求”的局面）和比较法（为什么人跳上速度不大的物体可以不发生相对滑动？因为人是可以形变、重心可以调节的特殊“物体”）

此外，本题的D选项还要用到匀变速运动规律。用匀变速运动规律和牛顿第二定律不难得出

只有当L ＞ 时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。

答案：A、D

思考：令L = 10m ，v = 2 m/s ，μ= 0.2 ，g取10 m/s2 ，试求工件到达皮带右端的时间t（过程略，答案为5.5s）

进阶练习：在上面“思考”题中，将工件给予一水平向右的初速v0 ，其它条件不变，再求t（学生分以下三组进行）——

① v0 = 1m/s  (答：0.5 + 37/8 = 5.13s)

② v0 = 4m/s  (答：1.0 + 3.5 = 4.5s)

③ v0 = 1m/s  (答：1.55s)

2、质量均为m的两只钩码A和B，用轻弹簧和轻绳连接，然后挂在天花板上，如图2所示。试问：

① 如果在P处剪断细绳，在剪断瞬时，B的加速度是多少？

② 如果在Q处剪断弹簧，在剪断瞬时，B的加速度又是多少？

解说：第①问是常规处理。由于“弹簧不会立即发生形变”，故剪断瞬间弹簧弹力维持原值，所以此时B钩码的加速度为零（A的加速度则为2g）。

第②问需要我们反省这样一个问题：“弹簧不会立即发生形变”的原因是什么？是A、B两物的惯性，且速度v和位移s不能突变。但在Q点剪断弹簧时，弹簧却是没有惯性的（没有质量），遵从理想模型的条件，弹簧应在一瞬间恢复原长！即弹簧弹力突变为零。

答案：0 ；g 。

二、牛顿第二定律的应用

应用要点：受力较少时，直接应用牛顿第二定律的“矢量性”解题。受力比较多时，结合正交分解与“独立作用性”解题。

在难度方面，“瞬时性”问题相对较大。

1、滑块在固定、光滑、倾角为θ的斜面上下滑，试求其加速度。

解说：受力分析 → 根据“矢量性”定合力方向 → 牛顿第二定律应用

答案：gsinθ。

思考：如果斜面解除固定，上表仍光滑，倾角仍为θ，要求滑块与斜面相对静止，斜面应具备一个多大的水平加速度？（解题思路完全相同，研究对象仍为滑块。但在第二环节上应注意区别。答：gtgθ。）

进阶练习1：在一向右运动的车厢中，用细绳悬挂的小球呈现如图3所示的稳定状态，试求车厢的加速度。（和“思考”题同理，答：gtgθ。）

进阶练习2、如图4所示，小车在倾角为α的斜面上匀加速运动，车厢顶用细绳悬挂一小球，发现悬绳与竖直方向形成一个稳定的夹角β。试求小车的加速度。

解：继续贯彻“矢量性”的应用，但数学处理复杂了一些（正弦定理解三角形）。

分析小球受力后，根据“矢量性”我们可以做如图5所示的平行四边形，并找到相应的夹角。设张力T与斜面方向的夹角为θ，则

θ=（90°+ α）- β= 90°-（β-α）                 （1）

对灰色三角形用正弦定理，有

 =                                        （2）

解（1）（2）两式得：ΣF = 

最后运用牛顿第二定律即可求小球加速度（即小车加速度）

答： 。

2、如图6所示，光滑斜面倾角为θ，在水平地面上加速运动。斜面上用一条与斜面平行的细绳系一质量为m的小球，当斜面加速度为a时（a＜ctgθ），小球能够保持相对斜面静止。试求此时绳子的张力T 。

解说：当力的个数较多，不能直接用平行四边形寻求合力时，宜用正交分解处理受力，在对应牛顿第二定律的“独立作用性”列方程。

正交坐标的选择，视解题方便程度而定。

解法一：先介绍一般的思路。沿加速度a方向建x轴，与a垂直的方向上建y轴，如图7所示（N为斜面支持力）。于是可得两方程

ΣFx = ma ，即Tx － Nx = ma

ΣFy = 0 ， 即Ty + Ny = mg

代入方位角θ，以上两式成为

T cosθ－N sinθ = ma                       （1）

T sinθ + Ncosθ = mg                       （2）

这是一个关于T和N的方程组，解（1）（2）两式得：T = mgsinθ + ma cosθ

解法二：下面尝试一下能否独立地解张力T 。将正交分解的坐标选择为：x——斜面方向，y——和斜面垂直的方向。这时，在分解受力时，只分解重力G就行了，但值得注意，加速度a不在任何一个坐标轴上，是需要分解的。矢量分解后，如图8所示。

根据独立作用性原理，ΣFx = max

即：T － Gx = max

即：T － mg sinθ = m acosθ

显然，独立解T值是成功的。结果与解法一相同。

答案：mgsinθ + ma cosθ

思考：当a＞ctgθ时，张力T的结果会变化吗？（从支持力的结果N = mgcosθ－ma sinθ看小球脱离斜面的条件，求脱离斜面后，θ条件已没有意义。答：T = m 。）

学生活动：用正交分解法解本节第2题“进阶练习2”

进阶练习：如图9所示，自动扶梯与地面的夹角为30°，但扶梯的台阶是水平的。当扶梯以a = 4m/s2的加速度向上运动时，站在扶梯上质量为60kg的人相对扶梯静止。重力加速度g = 10 m/s2，试求扶梯对人的静摩擦力f 。

解：这是一个展示独立作用性原理的经典例题，建议学生选择两种坐标（一种是沿a方向和垂直a方向，另一种是水平和竖直方向），对比解题过程，进而充分领会用牛顿第二定律解题的灵活性。

答：208N 。

3、如图10所示，甲图系着小球的是两根轻绳，乙图系着小球的是一根轻弹簧和轻绳，方位角θ已知。现将它们的水平绳剪断，试求：在剪断瞬间，两种情形下小球的瞬时加速度。

解说：第一步，阐明绳子弹力和弹簧弹力的区别。

（学生活动）思考：用竖直的绳和弹簧悬吊小球，并用竖直向下的力拉住小球静止，然后同时释放，会有什么现象？原因是什么？

结论——绳子的弹力可以突变而弹簧的弹力不能突变（胡克定律）。

第二步，在本例中，突破“绳子的拉力如何瞬时调节”这一难点（从即将开始的运动来反推）。

知识点，牛顿第二定律的瞬时性。

答案：a甲 = gsinθ ；a乙 = gtgθ 。

应用：如图11所示，吊篮P挂在天花板上，与吊篮质量相等的物体Q被固定在吊篮中的轻弹簧托住，当悬挂吊篮的细绳被烧断瞬间，P、Q的加速度分别是多少？

解：略。

答：2g ；0 。

三、牛顿第二、第三定律的应用

要点：在动力学问题中，如果遇到几个研究对象时，就会面临如何处理对象之间的力和对象与外界之间的力问题，这时有必要引进“系统”、“内力”和“外力”等概念，并适时地运用牛顿第三定律。

在方法的选择方面，则有“隔离法”和“整体法”。前者是根本，后者有局限，也有难度，但常常使解题过程简化，使过程的物理意义更加明晰。

对N个对象，有N个隔离方程和一个（可能的）整体方程，这（N + 1）个方程中必有一个是通解方程，如何取舍，视解题方便程度而定。

补充：当多个对象不具有共同的加速度时，一般来讲，整体法不可用，但也有一种特殊的“整体方程”，可以不受这个局限（可以介绍推导过程）——

Σ= m1 + m2 + m3 + … + mn

其中Σ只能是系统外力的矢量和，等式右边也是矢量相加。

1、如图12所示，光滑水平面上放着一个长为L的均质直棒，现给棒一个沿棒方向的、大小为F的水平恒力作用，则棒中各部位的张力T随图中x的关系怎样？

解说：截取隔离对象，列整体方程和隔离方程（隔离右段较好）。

答案：N = x 。

思考：如果水平面粗糙，结论又如何？

解：分两种情况，（1）能拉动；（2）不能拉动。

第（1）情况的计算和原题基本相同，只是多了一个摩擦力的处理，结论的化简也麻烦一些。

第（2）情况可设棒的总质量为M ，和水平面的摩擦因素为μ，而F = μMg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。

答：若棒仍能被拉动，结论不变。

若棒不能被拉动，且F = μMg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 〔x -〈L-l〉〕。

应用：如图13所示，在倾角为θ的固定斜面上，叠放着两个长方体滑块，它们的质量分别为m1和m2 ，它们之间的摩擦因素、和斜面的摩擦因素分别为μ1和μ2 ，系统释放后能够一起加速下滑，则它们之间的摩擦力大小为：

A、μ1 m1gcosθ ；    B、μ2 m1gcosθ ；

C、μ1 m2gcosθ ；    D、μ1 m2gcosθ ；

解：略。

答：B 。（方向沿斜面向上。）

思考：（1）如果两滑块不是下滑，而是以初速度v0一起上冲，以上结论会变吗？（2）如果斜面光滑，两滑块之间有没有摩擦力？（3）如果将下面的滑块换成如图14所示的盒子，上面的滑块换成小球，它们以初速度v0一起上冲，球应对盒子的哪一侧内壁有压力？

解：略。

答：（1）不会；（2）没有；（3）若斜面光滑，对两内壁均无压力，若斜面粗糙，对斜面上方的内壁有压力。

2、如图15所示，三个物体质量分别为m1 、m2和m3 ，带滑轮的物体放在光滑水平面上，滑轮和所有接触面的摩擦均不计，绳子的质量也不计，为使三个物体无相对滑动，水平推力F应为多少？

解说：

此题对象虽然有三个，但难度不大。隔离m2 ，竖直方向有一个平衡方程；隔离m1 ，水平方向有一个动力学方程；整体有一个动力学方程。就足以解题了。

答案：F =  。

思考：若将质量为m3物体右边挖成凹形，让m2可以自由摆动（而不与m3相碰），如图16所示，其它条件不变。是否可以选择一个恰当的F′，使三者无相对运动？如果没有，说明理由；如果有，求出这个F′的值。

解：此时，m2的隔离方程将较为复杂。设绳子张力为T ，m2的受力情况如图，隔离方程为：

 = m2a

隔离m1 ，仍有：T = m1a

解以上两式，可得：a = g

最后用整体法解F即可。

答：当m1 ≤ m2时，没有适应题意的F′；当m1 ＞ m2时，适应题意的F′=  。

3、一根质量为M的木棒，上端用细绳系在天花板上，棒上有一质量为m的猫，如图17所示。现将系木棒的绳子剪断，同时猫相对棒往上爬，但要求猫对地的高度不变，则棒的加速度将是多少？

解说：法一，隔离法。需要设出猫爪抓棒的力f ，然后列猫的平衡方程和棒的动力学方程，解方程组即可。

法二，“新整体法”。

据Σ= m1 + m2 + m3 + … + mn ，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：

（ M + m ）g = m·0 + M a1 

解棒的加速度a1十分容易。

答案：g 。

四、特殊的连接体

当系统中各个体的加速度不相等时，经典的整体法不可用。如果各个体的加速度不在一条直线上，“新整体法”也将有一定的困难（矢量求和不易）。此时，我们回到隔离法，且要更加注意找各参量之间的联系。

解题思想：抓某个方向上加速度关系。方法：“微元法”先看位移关系，再推加速度关系。、

1、如图18所示，一质量为M 、倾角为θ的光滑斜面，放置在光滑的水平面上，另一个质量为m的滑块从斜面顶端释放，试求斜面的加速度。

解说：本题涉及两个物体，它们的加速度关系复杂，但在垂直斜面方向上，大小是相等的。对两者列隔离方程时，务必在这个方向上进行突破。

（学生活动）定型判断斜面的运动情况、滑块的运动情况。

位移矢量示意图如图19所示。根据运动学规律，加速度矢量a1和a2也具有这样的关系。

（学生活动）这两个加速度矢量有什么关系？

沿斜面方向、垂直斜面方向建x 、y坐标，可得：

a1y = a2y             ①

且：a1y = a2sinθ     ②

隔离滑块和斜面，受力图如图20所示。

对滑块，列y方向隔离方程，有：

mgcosθ- N = ma1y     ③

对斜面，仍沿合加速度a2方向列方程，有：

Nsinθ= Ma2          ④

解①②③④式即可得a2 。

答案：a2 =  。

（学生活动）思考：如何求a1的值？

解：a1y已可以通过解上面的方程组求出；a1x只要看滑块的受力图，列x方向的隔离方程即可，显然有mgsinθ= ma1x ，得:a1x = gsinθ 。最后据a1 = 求a1 。

答：a1 =  。

2、如图21所示，与水平面成θ角的AB棒上有一滑套C ，可以无摩擦地在棒上滑动，开始时与棒的A端相距b ，相对棒静止。当棒保持倾角θ不变地沿水平面匀加速运动，加速度为a（且a＞gtgθ）时，求滑套C从棒的A端滑出所经历的时间。

解说：这是一个比较特殊的“连接体问题”，寻求运动学参量的关系似乎比动力学分析更加重要。动力学方面，只需要隔离滑套C就行了。

（学生活动）思考：为什么题意要求a＞gtgθ？（联系本讲第二节第1题之“思考题”）

定性绘出符合题意的运动过程图，如图22所示：S表示棒的位移，S1表示滑套的位移。沿棒与垂直棒建直角坐标后，S1x表示S1在x方向上的分量。不难看出：

S1x + b = S cosθ                   ①

设全程时间为t ，则有：

S = at2                          ②

S1x = a1xt2                        ③

而隔离滑套，受力图如图23所示，显然：

mgsinθ= ma1x                       ④

解①②③④式即可。

答案：t = 

另解：如果引进动力学在非惯性系中的修正式 Σ+ * = m （注：*为惯性力），此题极简单。过程如下——

以棒为参照，隔离滑套，分析受力，如图24所示。

注意，滑套相对棒的加速度a相是沿棒向上的，故动力学方程为：

F*cosθ- mgsinθ= ma相            （1）

其中F* = ma                      （2）

而且，以棒为参照，滑套的相对位移S相就是b ，即：

b = S相 = a相 t2                 （3）

解（1）（2）（3）式就可以了。

第二讲 配套例题选讲

教材范本：龚霞玲主编《奥林匹克物理思维训练教材》，知识出版社，2002年8月第一版。

例题选讲针对“教材”第三章的部分例题和习题。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网