题目内容
 如图为一示波管中的水平偏转极板,已知极板的长度为L,两板距离为d,所加偏转电压为U,且下板带正电;若一束电子以初速v0沿极板的中线进入偏转电场,最终电子从P点飞出.设电子的质量为m,电量为e,不计电子的重力.试求
如图为一示波管中的水平偏转极板,已知极板的长度为L,两板距离为d,所加偏转电压为U,且下板带正电;若一束电子以初速v0沿极板的中线进入偏转电场,最终电子从P点飞出.设电子的质量为m,电量为e,不计电子的重力.试求(1)电子在极板间运动的加速度大小;
(2)电子通过极板发生的偏转距离y;
(3)若规定图中的上极板电势为零,试求P点的电势.
分析:(1)先求出电场力,再根据牛顿第二定律求解加速度;
(2)粒子做类似平抛运动,将粒子的运动沿初速度方向和电场力方向正交分解,根据运动学规律列式求解;
(3)先求解电场强度,再求解上极板与P点的电势差,最后求解P点的电势.
(2)粒子做类似平抛运动,将粒子的运动沿初速度方向和电场力方向正交分解,根据运动学规律列式求解;
(3)先求解电场强度,再求解上极板与P点的电势差,最后求解P点的电势.
解答:解:(1)极板间是匀强电场,根据电势差与场强的关系,有:U=Ed
由于不计电子的重力,电子只受到电场力,故电场力为:F=Eq=
故加速度为:a=
=
①
即电子在极板间运动的加速度大小为
.
(2)粒子做类似平抛运动,将粒子的运动沿初速度方向和电场力方向正交分解
沿着初速度方向,有
L=v0t ②
沿着电场力方向,有
y=
at2 ③
由①②③解得
y=
即电子通过极板发生的偏转距离y为
.
(3)根据匀强电场中电势差与电场强度的关系式,上极板与P点间的电势差为
U=E(
d+y) ④
由于
U=Up-0=Up ⑤
解得
Up=
?(
d+
)=
+
即规定图中的上极板电势为零时,P点的电势为
+
.
由于不计电子的重力,电子只受到电场力,故电场力为:F=Eq=
| eU |
| d |
故加速度为:a=
| F |
| m |
| eU |
| md |
即电子在极板间运动的加速度大小为
| eU |
| md |
(2)粒子做类似平抛运动,将粒子的运动沿初速度方向和电场力方向正交分解
沿着初速度方向,有
L=v0t ②
沿着电场力方向,有
y=
| 1 |
| 2 |
由①②③解得
y=
| euL2 | ||
2md
|
即电子通过极板发生的偏转距离y为
| euL2 | ||
2md
|
(3)根据匀强电场中电势差与电场强度的关系式,上极板与P点间的电势差为
U=E(
| 1 |
| 2 |
由于
U=Up-0=Up ⑤
解得
Up=
| U |
| d |
| 1 |
| 2 |
| eUL2 | ||
2md
|
| U |
| 2 |
| eU2L2 | ||
2md2
|
即规定图中的上极板电势为零时,P点的电势为
| U |
| 2 |
| eU2L2 | ||
2md2
|
点评:本题关键是将电子的类似平抛运动沿着平行初速度方向和垂直初速度方向进行正交分解,然后根据运动学规律、牛顿第二定律和电势差与场强的关系公式列式求解.

练习册系列答案
相关题目
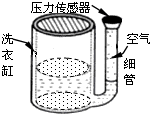 (1)当洗衣缸内水位缓慢升高时,设细管内空气温度不变,
(1)当洗衣缸内水位缓慢升高时,设细管内空气温度不变,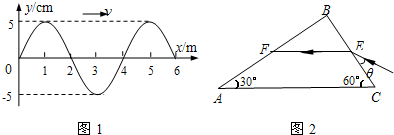
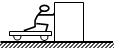 A.男孩和木箱组成的系统动量守恒
A.男孩和木箱组成的系统动量守恒 (3)如图所示,在竖直放置绝热圆柱形容器内用质量为m的绝热活塞密封一部分气体,活塞与容器壁间能无摩擦滑动,容器的横截面积为S,开始时密闭气体的温度为T0,活塞与容器底的距离为h0.现将整个装置放在大气压恒为P0的空气中,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,问:
(3)如图所示,在竖直放置绝热圆柱形容器内用质量为m的绝热活塞密封一部分气体,活塞与容器壁间能无摩擦滑动,容器的横截面积为S,开始时密闭气体的温度为T0,活塞与容器底的距离为h0.现将整个装置放在大气压恒为P0的空气中,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,问: 液反射后被接收,测出反射波的频率变化,就可知血液的流速.这
液反射后被接收,测出反射波的频率变化,就可知血液的流速.这  位移处,该波的传播方向为__▲___,波速为___▲____m/s.
位移处,该波的传播方向为__▲___,波速为___▲____m/s. (D)卢瑟福首先发现了质子和中子
(D)卢瑟福首先发现了质子和中子

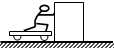
 (3)如图所示,在竖直放置绝热圆柱形容器内用质量为m的绝热活塞密封一部分气体,活塞与容器壁间能无摩擦滑动,容器的横截面积为S,开始时密闭气体的温度为T0,活塞与容器底的距离为h0.现将整个装置放在大气压恒为P0的空气中,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,问:
(3)如图所示,在竖直放置绝热圆柱形容器内用质量为m的绝热活塞密封一部分气体,活塞与容器壁间能无摩擦滑动,容器的横截面积为S,开始时密闭气体的温度为T0,活塞与容器底的距离为h0.现将整个装置放在大气压恒为P0的空气中,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,问: 液反射后被接收,测出反射波的频率变化,就可知血液的流速.这
液反射后被接收,测出反射波的频率变化,就可知血液的流速.这  位移处,该波的传播方向为__▲___,波速为___▲____m/s.
位移处,该波的传播方向为__▲___,波速为___▲____m/s. .求光在棱镜中传
.求光在棱镜中传 (D)卢瑟福首先发现了质子和中子
(D)卢瑟福首先发现了质子和中子 .则另一块爆炸后瞬时的速度大小__▲__。
.则另一块爆炸后瞬时的速度大小__▲__。