题目内容
【题目】【物理-选修3-5】如图所示，水平地面上有两个静止的小物块a和b，其连线与墙垂直：a和b相距l；b与墙之间也相距l；a的质量为m，b的质量为 
m，两物块与地面间的动摩擦因数均相同，现使a以初速度 
向右滑动，此后a与b发生弹性碰撞，但b没有与墙发生碰撞，重力加速度大小为g，求物块与地面间的动摩擦力因数满足的条件。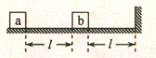
【答案】解：设物块与地面间的动摩擦因数为μ，若要物块a、b能够发生碰撞，应有 
即 
设在a、b发生弹性碰撞前的瞬间，a的速度大小为 
，由能量守恒可得 
设在a、b碰撞后的瞬间，a、b的速度大小分别为 
，
根据动量守恒和能量守恒可得 
， 
联立可得 
根据题意，b没有与墙发生碰撞，根据功能关系可知， 
故有 
，
综上所述，a与b发生碰撞，但b没有与墙发生碰撞的条件是 
【解析】由题意可得动摩擦因数必须满足两个条件：①a、b能相碰；②b不能与墙相碰．先根据能量求出a与b碰撞前的速度．再根据弹性碰撞过程遵守动量守恒和能量守恒列式，得到碰后b的速度，根据b没有与墙发生碰撞，碰后b向右滑行的距离s≤l，由功能列式，即可求解．
【考点精析】解答此题的关键在于理解动量守恒定律的相关知识，掌握动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．
练习册系列答案
相关题目
