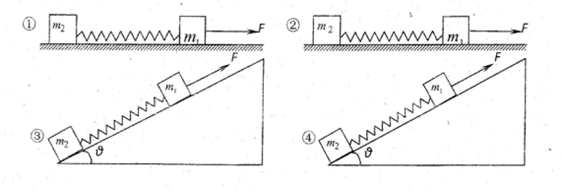
题目内容
如图所示,劲度系数为k2的轻质弹簧,竖直放在桌面上,上面压一质量为m的物体,另一劲度系数为k1的轻质弹簧竖直地放在物体上面,其下端与物块上表面连接在一起,要想物体在静止时,下面弹簧承受物重的2/3,应将上面弹簧持上端A竖直向上提高多大的距离?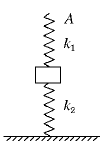
mg(k1+k2)/(3k1k2)
解决本题的关键是明确每根弹簧的状态变化,有效的办法是明确每根弹簧的初?末状态,必要时画出示意图.
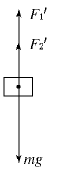
末态时物块受力分析如图所示,其中F1′与F2′分别是弹簧k1、k2的作用力,物块静止时有F1′+F2′=mg.
对于弹簧k2:
初态时,弹簧k2(压缩)的弹力F2=mg
末态时,弹簧k2(压缩)的弹力F2′=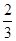
mg,弹簧k2的长度变化量为
Δx2=ΔF2/k2=(F2-F2′)/k2=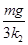
对弹簧k1:
初态时,弹簧k1(原长)的弹力F1=0
末态时,弹簧k1(伸长)的弹力F1′=mg/3
弹簧k1的长度变化量
Δx1=ΔF1/k1=(F1′-F1)/k1=mg/(3k1)
由几何关系知所求距离为:
Δx1+Δx2=mg(k1+k2)/(3k1k2).
末态时物块受力分析如图所示,其中F1′与F2′分别是弹簧k1、k2的作用力,物块静止时有F1′+F2′=mg.
对于弹簧k2:
初态时,弹簧k2(压缩)的弹力F2=mg
末态时,弹簧k2(压缩)的弹力F2′=
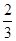mg,弹簧k2的长度变化量为Δx2=ΔF2/k2=(F2-F2′)/k2=
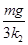
对弹簧k1:
初态时,弹簧k1(原长)的弹力F1=0
末态时,弹簧k1(伸长)的弹力F1′=mg/3
弹簧k1的长度变化量
Δx1=ΔF1/k1=(F1′-F1)/k1=mg/(3k1)
由几何关系知所求距离为:
Δx1+Δx2=mg(k1+k2)/(3k1k2).
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
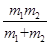m1g 
)g
