��Ŀ����
5�������˶��ڸ��������˶���Ŀ�кܳ�������ƹ�����˶���������ƹ���������⣬����̨��2L������h��ƹ����ǰ��ˮƽ���ٶȲ��䣬��ֱ���ٶȴ�С���䡢�����෴���Ҳ�����ƹ�������ת�Ϳ��������������������ٶ�Ϊg��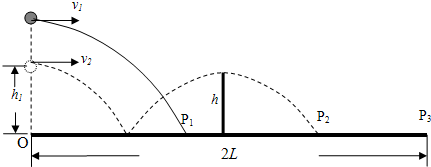
��1����������̨��ԵO�����Ϸ��߶�Ϊh1�����ٶ�v1��ˮƽ������������̨��P1�㣨��ͼʵ����ʾ������P1���O��ľ���x1��
��2��������O�����Ϸ����ٶ�v2ˮƽ������ǡ������ߵ�ʱԽ������������̨��P2����ͼ������ʾ������v2�Ĵ�С��
��3��������O���Ϸ�ˮƽ����������ǡ��Խ�������Ҹպ����ڶԷ���̨��ԵP3��������O��ĸ߶�h3��
���� ��1�����ݸ߶����ƽ���˶���ʱ�䣬�ٸ��ݳ��ٶȺ�ʱ�����ˮƽλ�ƣ�
��2��������O�����Ϸ����ٶ�v2ˮƽ������ǡ������ߵ�ʱԽ��������֪ƽ�ĸ߶ȵ������ߣ��Ӷ���֪ƽ���˶���ʱ�䣬�����˶��ĶԳ������ƽ���˶���λ�ƣ��ٸ���ˮƽλ�ƺ�ʱ�����ƽ�ij��ٶȣ�
��3�����������˶����ص����С��Խ������������ߵ��ˮƽλ�ƣ��Ӷ���֪С����Խ����ʱ��ˮƽλ�ƣ��Է������˶���ȡ����˼ά��ץסˮƽ�������ֱ�����˶��ĵ�ʱ�����С��Խ������������ߵ����ֱλ����������ֱλ�Ƶı�ֵ���Ӷ����������O��ĸ߶ȣ�
��� �⣺��1���跢��ʱ����ʱ��Ϊt1������ƽ���˶��У�${h_1}=\frac{1}{2}gt_1^2$
x1=v1t1
��ã�${x_1}={{v}_1}\sqrt{\frac{{2{h_1}}}{g}}$
��2���跢��߶�Ϊh2������ʱ��Ϊt2��ͬ���У�
${h_2}=\frac{1}{2}gt_2^2$
x2=v2t2
��h2=h
2x2=L
�ã�${{v}_2}=\frac{L}{2}\sqrt{\frac{g}{2h}}$
��3�������ǡ��Խ����������ߵ��ʱ��Ϊt��ˮƽ����Ϊs�����������˶����ص㼰�����ĶԳ��ԣ�֪��������ߵ��ˮƽλ��Ϊ$\frac{2L}{3}$������Խ��������ˮƽλ��Ϊ$L-\frac{2L}{3}=\frac{1}{3}L$����ͼ�е�s=$\frac{1}{3}L$����ˮƽ������������ֱ���˶������Դ�Խ����������ߵ����õ�ʱ��ʹӷ�������ߵ��ʱ���Ϊ1��2��
�Է�������ߵ���˶���ȡ����˼ά������ˮƽ�����ϵ��˶�����ֱ�����ϵ��˶����е�ʱ�ԣ�֪Խ����������ߵ���ֱ�����ϵ�ʱ��ͷ�������ߵ�����ֱ�����ϵ�ʱ���Ϊ1��2������h=$\frac{1}{2}g{t}^{2}$�ã�֪Խ����������ߵ���ֱ�����ϵ�λ�ƺͷ�������ߵ��λ��Ϊ1��4����$\frac{{h}_{3}-h}{{h}_{3}}=\frac{1}{4}$��
��ã�${h}_{3}=\frac{4}{3}h$��
�𣺣�1��P1���O��ľ���Ϊ${x}_{1}={v}_{1}\sqrt{\frac{2{h}_{1}}{g}}$��
��2��v2�Ĵ�СΪ${v}_{2}=\frac{L}{2}\sqrt{\frac{g}{2h}}$��
��3��������O��ĸ߶�h3Ϊ$\frac{4}{3}h$��
���� �������Ĺؼ�֪��ƽ���˶���ˮƽ�������ֱ�����ϵ��˶����ɣ�����˶�ѧ��ʽ�����⣬�Ѷ��еȣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��R=$\frac{U}{I}$��֪������һ��ȷ���ĵ�����˵�����ͨ���ĵ���Խ���������˵ĵ�ѹҲԽ�� | |
| B�� | ��I=$\frac{U}{R}$֪�������еĵ���ǿ�ȸ��������˵ĵ�ѹ�����ȣ�������ĵ���ɷ��� | |
| C�� | ��R=$\frac{U}{I}$��֪������ĵ�����������˵ĵ�ѹ�����ȣ��������еĵ���ǿ�ȳɷ��� | |
| D�� | ��һ��ȷ���ĵ�����������ֵ$\frac{U}{I}$�㶨������U��I�ĸı���ı� |
 ��ͼ��ʾ���ڴֲڵ�������һ����A��������ͨ������������������ʹ����A��������ֱ���˶�����ˮƽ����F�Ĵ�С�仯��������ǣ�������
��ͼ��ʾ���ڴֲڵ�������һ����A��������ͨ������������������ʹ����A��������ֱ���˶�����ˮƽ����F�Ĵ�С�仯��������ǣ�������| A�� | ��� | B�� | ��С | C�� | �ȱ���С | D�� | �ȱ�С������ |

| A�� | �˶�Ա���䵽�սӴ��Ĵ�ʱ���ٶ���� | |
| B�� | �˶�����͵�ʱ�������˶�Ա�������������˶�Ա�Դ��������� | |
| C�� | �ӸսӴ��Ĵ����˶�����͵�Ĺ����У��˶�Աһֱ���ڳ���״̬���˶�Ա�ļ��ٶ��ȼ�С������ | |
| D�� | ����������У��������˶�Ա�����Ĺ��������������ܵļ�С |
| A�� | �糡ǿ��E��F�����ȣ���q�ɷ��� | |
| B�� | �糡�еĵ��������ĵ�����仯��$\frac{F}{q}$��ֵҲ�仯 | |
| C�� | �糡��ij��ij�ǿΪ�㣬���ڸõ�ĵ���ܵ��ĵ糡��һ��Ϊ�� | |
| D�� | һ���������С����P���ܵ��ĵ糡��Ϊ�㣬��P��ij�ǿһ��Ϊ�� |
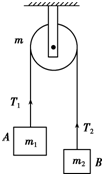 ��ͼ��ʾ��һ�����쳤������ϸ����������ֺ����˷ֱ���������Ϊm1��m2������A��B����������һ����С������Ϊm�ҷֲ����ȣ�����ת��ʱ����֮������Ի��������ƻ�������֮���ĥ������ϸ����A��B��������С�ֱ�ΪT1��T2����֪�����ĸ�������T1�ı���ʽ����һ������ȷ�ģ����������ѧ������֪ʶ��ͨ��һ���ķ������ж���ȷ�ı���ʽ�ǣ�������
��ͼ��ʾ��һ�����쳤������ϸ����������ֺ����˷ֱ���������Ϊm1��m2������A��B����������һ����С������Ϊm�ҷֲ����ȣ�����ת��ʱ����֮������Ի��������ƻ�������֮���ĥ������ϸ����A��B��������С�ֱ�ΪT1��T2����֪�����ĸ�������T1�ı���ʽ����һ������ȷ�ģ����������ѧ������֪ʶ��ͨ��һ���ķ������ж���ȷ�ı���ʽ�ǣ�������| A�� | T1=$\frac{��m+2{m}_{2}��{m}_{1}g}{m+2��{m}_{1}+{m}_{2}��}$ | B�� | T1=$\frac{��m+2{m}_{1}��{m}_{1}g}{m+4��{m}_{1}+{m}_{2}��}$ | ||
| C�� | T1=$\frac{��m+4{m}_{2}��{m}_{1}g}{m+2��{m}_{1}+{m}_{2}��}$ | D�� | T1=$\frac{��m+4{m}_{1}��{m}_{2}g}{m+4��{m}_{1}+{m}_{2}��}$ |
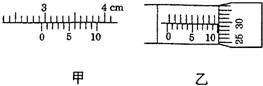 ������ͼ��ʾ���α꿨�ߣ��α������10���ȷ̶ֿȣ�������������ʾ����ͼ�Ķ���Ϊ2.96cm��ͼ�ҵĶ���Ϊ10.295mm��
������ͼ��ʾ���α꿨�ߣ��α������10���ȷ̶ֿȣ�������������ʾ����ͼ�Ķ���Ϊ2.96cm��ͼ�ҵĶ���Ϊ10.295mm��