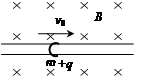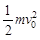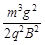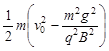题目内容
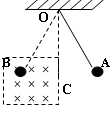
如图所示,在直角坐标系xoy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的正电粒子,位于y轴的右侧垂直于x轴有一长度为L的很薄的荧光屏MN,荧光屏正反两侧均涂有荧光粉,MN与x轴交于O'点。已知三角形MNO为正三角形,放射源S射出的粒子质量为m,带电荷量为q,速度大小为v,不计粒子的重力。
(1)若只在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧射出的所有粒子都能打到荧光屏MN上,试求电场强度的最小值Emin及此条件下打到荧光屏M点的粒子的动能;
(2)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,要使粒子能打到荧光屏MN的反面 O'点,试求磁场的磁感应强度的最大值Bmax;
(3)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,磁感应强度与(2)题中所求Bmax相同,试求粒子打在荧光屏MN的正面O'点所需的时间t1和打在荧光屏MN的反面O'点所需的时间t2之比。
(1)若只在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧射出的所有粒子都能打到荧光屏MN上,试求电场强度的最小值Emin及此条件下打到荧光屏M点的粒子的动能;
(2)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,要使粒子能打到荧光屏MN的反面 O'点,试求磁场的磁感应强度的最大值Bmax;
(3)若在xOy平面内只加一方向垂直纸面向里的匀强磁场,磁感应强度与(2)题中所求Bmax相同,试求粒子打在荧光屏MN的正面O'点所需的时间t1和打在荧光屏MN的反面O'点所需的时间t2之比。

(1)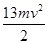 (2)
(2)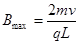 (3)
(3)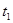 ∶
∶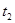 =1∶2
=1∶2
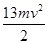 (2)
(2)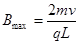 (3)
(3)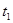 ∶
∶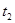 =1∶2
=1∶2 (1)所加电场电场强度的最小值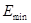 对应沿着
对应沿着 轴正方向射出的带电粒子正好打在荧光屏的端点
轴正方向射出的带电粒子正好打在荧光屏的端点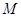 这一临界状态。对该临界态的粒子有
这一临界状态。对该临界态的粒子有
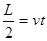 ,
,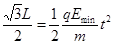 (3分)
(3分)
其中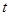 为该粒子运动的时间, 解得
为该粒子运动的时间, 解得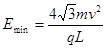 (2分)
(2分)
对此时从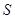 射出能打到荧光屏上的任一粒子(包括打到荧光屏
射出能打到荧光屏上的任一粒子(包括打到荧光屏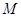 点的粒子),设它到达屏时的动能为
点的粒子),设它到达屏时的动能为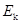 ,由动能定理有
,由动能定理有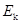 -
-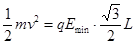 (2分)
(2分)
解得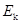 =
=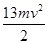 (2分)
(2分)
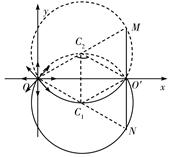
(2)由题意,所加磁场的最大磁感应强度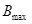 对应来自
对应来自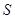 的粒子恰好经过荧光屏下端点N后打到
的粒子恰好经过荧光屏下端点N后打到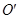 这一临界状态,如图所示(圆心在
这一临界状态,如图所示(圆心在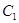 )。从图中的几何关系得,粒子在磁场中做圆周运动的半径
)。从图中的几何关系得,粒子在磁场中做圆周运动的半径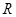 满足
满足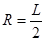 (2分)
(2分)
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,有
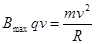 (2分)
(2分)
联立解得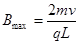 (1分)
(1分)
(3)打在荧光屏正面O点的粒子的圆弧轨迹见图(圆心在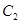 ),根据匀速圆周运动规律有
),根据匀速圆周运动规律有
 ,
,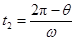 (2分)
(2分)
由图中的几何关系得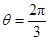 (2分)
(2分)
联立解得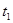 ∶
∶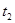 =1∶2 (1分)
=1∶2 (1分)
本题考查了带电粒子在磁场电场中运动,选好临界状态最关键,当加电场时所加电场电场强度的最小值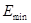 对应沿着
对应沿着 轴正方向射出的带电粒子正好打在荧光屏的端点
轴正方向射出的带电粒子正好打在荧光屏的端点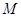 这一临界状态,当加磁场时所加磁场的最大磁感应强度
这一临界状态,当加磁场时所加磁场的最大磁感应强度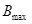 对应来自
对应来自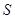 的粒子恰好经过荧光屏下端点N后打到
的粒子恰好经过荧光屏下端点N后打到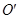 这一临界状态
这一临界状态
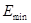 对应沿着
对应沿着 轴正方向射出的带电粒子正好打在荧光屏的端点
轴正方向射出的带电粒子正好打在荧光屏的端点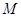 这一临界状态。对该临界态的粒子有
这一临界状态。对该临界态的粒子有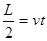 ,
,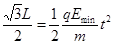 (3分)
(3分)其中
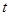 为该粒子运动的时间, 解得
为该粒子运动的时间, 解得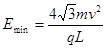 (2分)
(2分)对此时从
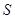 射出能打到荧光屏上的任一粒子(包括打到荧光屏
射出能打到荧光屏上的任一粒子(包括打到荧光屏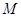 点的粒子),设它到达屏时的动能为
点的粒子),设它到达屏时的动能为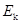 ,由动能定理有
,由动能定理有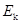 -
-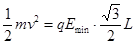 (2分)
(2分)解得
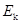 =
=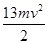 (2分)
(2分)
(2)由题意,所加磁场的最大磁感应强度
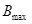 对应来自
对应来自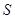 的粒子恰好经过荧光屏下端点N后打到
的粒子恰好经过荧光屏下端点N后打到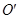 这一临界状态,如图所示(圆心在
这一临界状态,如图所示(圆心在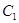 )。从图中的几何关系得,粒子在磁场中做圆周运动的半径
)。从图中的几何关系得,粒子在磁场中做圆周运动的半径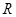 满足
满足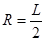 (2分)
(2分)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,有
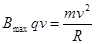 (2分)
(2分)联立解得
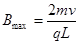 (1分)
(1分)(3)打在荧光屏正面O点的粒子的圆弧轨迹见图(圆心在
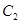 ),根据匀速圆周运动规律有
),根据匀速圆周运动规律有 ,
,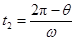 (2分)
(2分)由图中的几何关系得
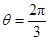 (2分)
(2分) 联立解得
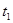 ∶
∶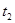 =1∶2 (1分)
=1∶2 (1分)本题考查了带电粒子在磁场电场中运动,选好临界状态最关键,当加电场时所加电场电场强度的最小值
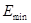 对应沿着
对应沿着 轴正方向射出的带电粒子正好打在荧光屏的端点
轴正方向射出的带电粒子正好打在荧光屏的端点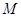 这一临界状态,当加磁场时所加磁场的最大磁感应强度
这一临界状态,当加磁场时所加磁场的最大磁感应强度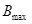 对应来自
对应来自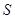 的粒子恰好经过荧光屏下端点N后打到
的粒子恰好经过荧光屏下端点N后打到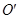 这一临界状态
这一临界状态
练习册系列答案
相关题目