题目内容
用长为l的细线拴一个小球使其绕细线的加一端在竖直平面内做圆周运动,当球通过圆周的最高点时,细线受到的拉力等于球重的2倍,已知重力加速度为g,则球此时的速度大小为 ,角速度大小为 ,加速度大小为 .
【答案】分析:小球在最高点,靠竖直方向上的合力提供向心力,根据牛顿第二定律求出小球在最高点的速度,从而根据速度与角速度的关系求出角速度的大小,根据向心力的公式求出加速度的大小.
解答:解:根据牛顿第二定律得,T+mg=m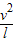 ,解得v=
,解得v=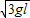 .
.
角速度ω=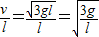 .
.
加速度a= .
.
故答案为: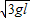 ;
;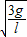 ;3g
;3g
点评:解决本题的关键搞清圆周运动向心力的来源,结合牛顿第二定律进行求解.
解答:解:根据牛顿第二定律得,T+mg=m
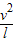 ,解得v=
,解得v=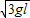 .
.角速度ω=
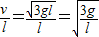 .
.加速度a=
 .
.故答案为:
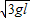 ;
;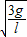 ;3g
;3g点评:解决本题的关键搞清圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
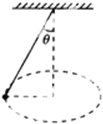 如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法正确的是( )
如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法正确的是( )| A、小球受到重力、线的拉力和向心力三个力 | B、向心力的大小等于细线对小球拉力的大小 | C、向心力的大小等于重力的大小 | D、向心力是细线的拉力和小球所受重力的合力 |
 如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法错误的是( )
如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法错误的是( ) 如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为0,关于小球的受力情况,下列说法正确的是( )
如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为0,关于小球的受力情况,下列说法正确的是( )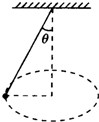 如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法正确的是( )
如图所示,用长为L的细线拴一个质量为M的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向间的夹角为θ,关于小球的受力情况,下列说法正确的是( )