��Ŀ����
4�� ��ͼ��һ����m=0.5kg��С����Ϊ�ʵ㣩��ij�ߴ�A�Գ��ٶ�v0=4m/sˮƽ�׳����˶�һ��ˮƽλ�ƺ�ǡ��Բ��������߽���һ����ֱԲ��������е�ΪB��Բ���뾶R=0.5m��С�����Բ���������Բ���˶���OB����ֱ����н�37�㣬��֪С���˶�����͵�C���ٶ�Ϊ8m/s��gȡ10m/s2��sin37��=0.6��cos37��=0.8�����𰸿����ø��ű�ʾ��
��ͼ��һ����m=0.5kg��С����Ϊ�ʵ㣩��ij�ߴ�A�Գ��ٶ�v0=4m/sˮƽ�׳����˶�һ��ˮƽλ�ƺ�ǡ��Բ��������߽���һ����ֱԲ��������е�ΪB��Բ���뾶R=0.5m��С�����Բ���������Բ���˶���OB����ֱ����н�37�㣬��֪С���˶�����͵�C���ٶ�Ϊ8m/s��gȡ10m/s2��sin37��=0.6��cos37��=0.8�����𰸿����ø��ű�ʾ����1����͵�C����С��Թ��ѹ����С��
��2��A�����ֱ�߶�h��С��
��3����С��ǡ��ͨ����ߵ�Dƽ�׳�ȥ�������˶���B��ȸ�ʱ���ٶ�vt�Ƕ��
���� ��1������͵�C����С���ܵ����������֧�������ɶ����ĺ����ṩ����������ţ�ٵڶ�����������֧�������ٵõ�С��Թ����ѹ����
��2��С��B����ٶ��ع�����߷����ٶȷֽ⣬���B�����ֱ���ٶȣ������˶�ѧ��ʽ���h��
��3��С����D���������ṩ�����������D����ٶȣ�����ƽ���˶��Ĺ������ٶ�vt��
���  �⣺��1��С����C����������֧��������ţ�ٵڶ����ɵ�
�⣺��1��С����C����������֧��������ţ�ٵڶ����ɵ�
N-mg=m$\frac{{v}_{C}^{2}}{R}$
��� N=69N
��ţ�ٵ������ɵã�С��Թ��ѹ�� N��=69N
��2����B���ٶȷֽ�ͼ vy=v0tan37��=3m/s
���� h=$\frac{{v}_{y}^{2}}{2g}$+R��1-cos37�㣩
��� h=0.55m
��3��С����D���������ṩ����������
mg=m$\frac{{v}_{D}^{2}}{R}$
�� vD=$\sqrt{5}$m/s
ƽ����B��ȸ�ʱ�½��߶� h��=R+Rcos37��=0.9m
��ֱ���ٶ� ${v}_{y}^{��}$=$\sqrt{2gh��}$
��ô�ʱ�ٶ� vt=$\sqrt{{v}_{D}^{2}+{v}_{y}^{��2}}$=$\sqrt{5+18}$=$\sqrt{23}$m/s
��
��1����͵�C����С��Թ��ѹ����С��69N��
��2��A�����ֱ�߶�h��С��0.55m��
��3����С��ǡ��ͨ����ߵ�Dƽ�׳�ȥ�������˶���B��ȸ�ʱ���ٶ�vt��$\sqrt{23}$m/s��
���� ������ƽ���˶���Բ���˶����ϵĵ�����Ŀ����������ƽ���˶���Բ���˶��Ļ�����ʽ�⣬�ؼ�Ҫ����D����ٽ�����������������������

 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�| A�� | n�� | B�� | n2�� | C�� | $\frac{n}{2}$�� | D�� | $\frac{{n}^{2}}{4}$�� |
 ��ͼ��ʾ����һ�οյ���ϰ�У����H�ߴ��ķɻ���ˮƽ�ٶ�v1����һ���ڵ�����ը����Ŀ��P����Ӧ�����ĵ�������ϵͳͬʱ���ٶ�v2��ֱ���Ϸ����ڵ����أ�������ϵͳ��ɻ���ˮƽ����Ϊs�������سɹ������ƿ�����������v1��v2 �Ĺ�ϵӦ���㣨������
��ͼ��ʾ����һ�οյ���ϰ�У����H�ߴ��ķɻ���ˮƽ�ٶ�v1����һ���ڵ�����ը����Ŀ��P����Ӧ�����ĵ�������ϵͳͬʱ���ٶ�v2��ֱ���Ϸ����ڵ����أ�������ϵͳ��ɻ���ˮƽ����Ϊs�������سɹ������ƿ�����������v1��v2 �Ĺ�ϵӦ���㣨������| A�� | v1=v2 | B�� | v1=$\frac{H}{s}$v2 | C�� | v1=$\sqrt{\frac{H}{s}}{v_2}$ | D�� | v1=$\frac{s}{H}{v_2}$ |
| A�� | һ�����ض���ϵ���������壬����ÿ���������������������ʩ������ | |
| B�� | �����ķ���һ����ֱ�ڽӴ������� | |
| C�� | ����Ӵ�������һ������Ħ���� | |
| D�� | ������ʱ�Ƕ�������ʱ����������Ħ������������ |
| A�� | 1m/s2��5m/s | B�� | 2m/s2��5m/s | C�� | 1m/s2��10m/s | D�� | 2m/s2��10m/s |
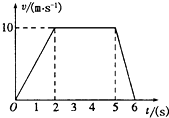 ij������ֱ���˶�����v-tͼ����ͼ��ʾ������ͼ����������⣺
ij������ֱ���˶�����v-tͼ����ͼ��ʾ������ͼ����������⣺