题目内容
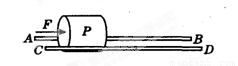
三角形传送带以1m/s的速度逆时针匀速转动，两边的传送带长都是2m且与水平方向的夹角均为37°。现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑，物块与传送带间的动摩擦因数都是0.5，（g取10m/s2，sin37°=0.6，cos37°=0.8）下列说法正确的是：
A．物块A先到达传送带底端
B．物块A、B同时到达传送带底端
C．物块A、B到达传送带底端时速度大小相等
D．物块A、B在传送带上的划痕长度之比为1:3
BCD
【解析】
试题分析：分析A受力可知，A物体重力的下滑分量大于滑动摩擦力，即相对于皮带向下加速，加速度为：
，分析B的受力可知，B相对于皮带也是向下滑的，摩擦力向上，其加速度也表达为：
，可见两个物体的加速度相同，加速位移一样，由运动学公式
知，AB两物体滑到底端时时间相同，故A错误，B正确；由
可知到达底端的速度相同，C正确；划痕长度由相对位移决定，由以上方程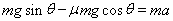
可以求得加速度为
，代人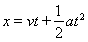
可以求得时间为
对A物体与传送带运动方向相同，
，B物体的划痕为：
，故物块A、B在传送带上的划痕长度之比为1:3，D正确。
考点：本题考查了牛顿第二定律和匀变速直线运动规律
练习册系列答案
相关题目
