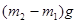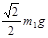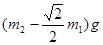题目内容
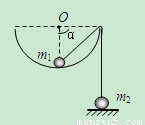
 B.如图所示,一个半径为R=0.45m的光滑半圆柱面固定在水平面上,在圆柱的最高点有一个小物体,以垂直于圆柱的方向、大小为υ0=1.2m/s的水平初速度离开最高点.求:小物体落地的位置?
B.如图所示,一个半径为R=0.45m的光滑半圆柱面固定在水平面上,在圆柱的最高点有一个小物体,以垂直于圆柱的方向、大小为υ0=1.2m/s的水平初速度离开最高点.求:小物体落地的位置?某同学的解答过程是:
小物体落地的时间 t=
| 2h/g |
| 2x0.45/10 |
小物体落地点离圆柱面的距离 s=υt=1.2m/s×0.3s=0.36m
你认为该同学的解答过程是否正确?请你说明理由,如果你认为不正确,也请说明理由.
分析:当小球仅受重力,有水平初速度时做平抛运动,根据牛顿第二定律求出小物体在最高点所受支持力为零时,小物体的速度,判断小物体是否做 平抛运动.
解答:解:不对.
因为小球在最高点对轨道压力为零时有:mg=m
,解得v0=
=
m/s>1.2m/s
小物体先沿圆柱面下滑一段距离后才离开圆柱面的,不是直接做平抛运动
的,故上述计算过程不正确
小物体先沿圆柱面下滑一段距离后才离开圆柱面的,不是直接做平抛运动
的,故上述计算过程不正确
所以小物体沿圆柱面下滑一段距离才离开圆柱面,不能直接做平抛运动,故上述解法错误.
答:不对,因为小球不能直接做平抛运动.
因为小球在最高点对轨道压力为零时有:mg=m
| v02 |
| R |
| gR |
| 4.5 |
小物体先沿圆柱面下滑一段距离后才离开圆柱面的,不是直接做平抛运动
的,故上述计算过程不正确
小物体先沿圆柱面下滑一段距离后才离开圆柱面的,不是直接做平抛运动
的,故上述计算过程不正确
所以小物体沿圆柱面下滑一段距离才离开圆柱面,不能直接做平抛运动,故上述解法错误.
答:不对,因为小球不能直接做平抛运动.
点评:解决本题的关键知道平抛运动的特点,以及会根据牛顿第二定律求出在最高点的临界速度.

练习册系列答案
相关题目
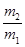 为 ( )
为 ( )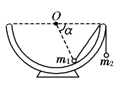
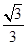
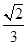
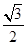

 为 (
)
为 (
)
 B.
B.
 D.
D.
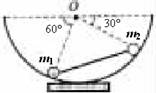
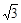 C.
C.