题目内容
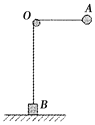
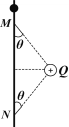
【题目】如图所示,光滑绝缘细杆竖直放置,细杆右侧距杆0.3 m处有一固定的点电荷Q,M、N是细杆上的两点,点M与Q、点N与Q的连线与杆的夹角均为θ=37°.一中间有孔的带电小球穿在绝缘细杆上滑下,通过M点时加速度为零,速度为3m/s,取g=10 m/s2,求小球下落到N点时的加速度大小和速度大小。
【答案】a=20m/s2,方向竖直向下;vN=5m/s
【解析】
试题分析:设小球在M点受到的电场力为F,则小球在N点受到的电场力也为F.
在M处,根据牛顿第二定律得:Fcosθ—mg=0 ①
在N处,根据牛顿第二定律得:Fcosθ+mg=ma ②
联立①②得:a=2g=20m/s2,方向竖直向下。
设M N两点的高度差为h,M、N两点位于同一等势面上,所以小球从M运动到N的过程中,电场力做功为零,由动能定理得:
mgh=![]() ③
③
由几何关系得:h=0.6cotθ ④
联立③④得:vN=5m/s

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
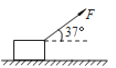
【题目】为了“探究加速度与力、质量的关系”,现提供了如图甲所示的实验装置.

(1)下列做法正确的有 .
A.平衡摩擦力时,用细线一端挂空桶,另一端与小车相连,将木板适当倾斜,使小车在木板上做匀速直线运动 |
B.在砂及桶总质量远小于小车及里面钩码的总质量时,可以近似认为小车受到的拉力等于砂及桶的重力 |
C.应让砂及桶总质量远大于小车及里面钩码的总质量 |
D.每次改变砂及桶总质量之后,应重新平衡摩擦力 |
(2)有一组同学保持小车及车中的砝码质量一定,探究加速度a与所受外力 F的关系,他们在轨道水平和倾斜两种情况下分别做了实验,得到了两条a﹣F图线,如图乙所示.图线 (选填“A”或“B”)是在长木板水平情况下得到的;小车和长木板间的动摩擦因数μ= (g取10m/s2).