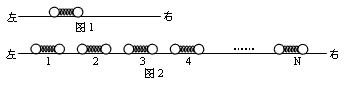题目内容
(1)如图1,在光滑水平长直轨道上,放着一个静止的弹簧振子,它由一轻弹簧两端各连接一个小球构成,两小球质量相等.现突然给左端小球一个向右的速度u0,求弹簧第一次恢复到自然长度时,每个小球的速度.
(2)如图2,将N个这样的振子放在该轨道上,最左边的振子1被压缩至弹簧为某一长度后锁定,静止在适当位置上,这时它的弹性势能为E0.其余各振子间都有一定的距离,现解除对振子1的锁定,任其自由运动,当它第一次恢复到自然长度时,刚好与振子2碰撞,此后,继续发生一系列碰撞,每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后,每个振子弹性势能的最大值.已知本题中两球发生碰撞时,速度交换,即一球碰后的速度等于另一球碰前的速度.

(2)如图2,将N个这样的振子放在该轨道上,最左边的振子1被压缩至弹簧为某一长度后锁定,静止在适当位置上,这时它的弹性势能为E0.其余各振子间都有一定的距离,现解除对振子1的锁定,任其自由运动,当它第一次恢复到自然长度时,刚好与振子2碰撞,此后,继续发生一系列碰撞,每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后,每个振子弹性势能的最大值.已知本题中两球发生碰撞时,速度交换,即一球碰后的速度等于另一球碰前的速度.

分析:(1)给左侧小球一初速度,弹簧被压缩后对两个小球都有弹力,左侧小球要减速,右侧小球要加速,由于两小球质量相等,故加速度相等,故右侧小球增加的速度等于左侧小球减小的速度,当速度相等时,弹簧被压的最短,此后,右侧小球进一步加速,左侧小球进一步减速,当弹簧恢复原长时,可以根据动量守恒定律和能量守恒定律列式求解出各个小球的速度;
(2)第一个弹簧振子在线断开后,两侧小球分别向两侧加速,右侧小球与第二个弹簧振子的左侧小球碰撞后静止,其动量完全传递给了第二个弹簧振子的左侧小球,此时第一个弹簧振子左侧小球有向左的动量,当两球速度相等时,第一个振子的弹簧最短,弹性势能最大;根据第一题的分析,当第二个弹簧振子的左侧小球速度为零时,其动量完全转移到第二个弹簧振子的右侧小球,然后第二个弹簧振子的右侧小球的动量又转移个下一个弹簧振子的左侧小球,然后在转移到右侧小球,循环下去,一直转移到最后一个弹簧振子的左侧小球,最后一个弹簧振子系统不会与其他系统碰撞,一直向右运动,其内部两个小球间动量不断的相互转移,与第一问中弹簧振子的运动情况相同,当两球速度相等时,弹簧最短,弹性势能最大.
(2)第一个弹簧振子在线断开后,两侧小球分别向两侧加速,右侧小球与第二个弹簧振子的左侧小球碰撞后静止,其动量完全传递给了第二个弹簧振子的左侧小球,此时第一个弹簧振子左侧小球有向左的动量,当两球速度相等时,第一个振子的弹簧最短,弹性势能最大;根据第一题的分析,当第二个弹簧振子的左侧小球速度为零时,其动量完全转移到第二个弹簧振子的右侧小球,然后第二个弹簧振子的右侧小球的动量又转移个下一个弹簧振子的左侧小球,然后在转移到右侧小球,循环下去,一直转移到最后一个弹簧振子的左侧小球,最后一个弹簧振子系统不会与其他系统碰撞,一直向右运动,其内部两个小球间动量不断的相互转移,与第一问中弹簧振子的运动情况相同,当两球速度相等时,弹簧最短,弹性势能最大.
解答:解:(1)设每个小球质量为m,以u1、u2分别表示弹簧恢复到自然长度时左右两端小球的速度.
由动量守恒和能量守恒定律有
mu1+mu2=mu0(以向右为速度正方向)
m
+
m
=
m
解得u1=u0,u2=0或u1=0,u2=u0
由于振子从初始状态到弹簧恢复到自然长度的过程中,弹簧一直是压缩状态,弹性力使左端小球持续减速,使右端小球持续加速,因此应该取解:u1=0,u2=u0
即弹簧第一次恢复到自然长度时,左侧小球速度为0,右侧小球速度为u0.
(2)以v1、v1′分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度,规定向右为速度的正方向,
由动量守恒和能量守恒定律,
mv1+mv1′=0
m
+
mv
=E0
解得
v1=
,v1′=-
或v1=-
,v1′=
在这一过程中,弹簧一直是压缩状态,弹性力使左端小球向左加速,右端小球向右加速,故应取解:v1=-
,v1′=
振子1与振子2碰撞后,由于交换速度,振子1右端小球速度变为0,左端小球速度仍为v1,此后两小球都向左运动,当它们向左的速度相同时,弹簧被拉伸至最长,弹性势能最大,设此速度为v10,根据动量守恒定律:
2mv10=mv1
用E1表示最大弹性势能,由能量守恒有
m
+
m
+E1=
m
解得
E1=
E0
振子2 被碰撞后瞬间,左端小球速度为
,右端小球速度为0.以后弹簧被压缩,当弹簧再恢复到自然长度时,根据(1)题结果,左端小球速度v2=0,右端小球速度v2′=
,与振子3碰撞,由于交换速度,振子2右端小球速度变为0,振子2静止,弹簧为自然长度,弹性势能为E2=0.
同样分析可得
E2=E3=…EN-1=0
振子N被碰撞后瞬间,左端小球速度 v′N-1=
,右端小球速度为0,弹簧处于自然长度.此后两小球都向右运动,弹簧被压缩,当它们向右的速度相同时,弹簧被压缩至最短,弹性势能最大.此速度为vN0,根据动量守恒定律,
2mvN0=mv?N-1
用EN表示最大弹性势能,根据能量守恒,有
m
+
m
+EN=
m
解得
EN=
E0
故所有可能的碰撞都发生后第一个弹簧振子的最大弹性势能为
E0,第二个到第N-1个弹簧振子的最大弹性势能为0,第N个弹簧振子的最大弹性势能为
E0.
由动量守恒和能量守恒定律有
mu1+mu2=mu0(以向右为速度正方向)
| 1 |
| 2 |
| u | 2 1 |
| 1 |
| 2 |
| u | 2 2 |
| 1 |
| 2 |
| u | 2 0 |
解得u1=u0,u2=0或u1=0,u2=u0
由于振子从初始状态到弹簧恢复到自然长度的过程中,弹簧一直是压缩状态,弹性力使左端小球持续减速,使右端小球持续加速,因此应该取解:u1=0,u2=u0
即弹簧第一次恢复到自然长度时,左侧小球速度为0,右侧小球速度为u0.
(2)以v1、v1′分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度,规定向右为速度的正方向,
由动量守恒和能量守恒定律,
mv1+mv1′=0
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| ′ | 2 1 |
解得
v1=
|
|
|
|
在这一过程中,弹簧一直是压缩状态,弹性力使左端小球向左加速,右端小球向右加速,故应取解:v1=-
|
|
振子1与振子2碰撞后,由于交换速度,振子1右端小球速度变为0,左端小球速度仍为v1,此后两小球都向左运动,当它们向左的速度相同时,弹簧被拉伸至最长,弹性势能最大,设此速度为v10,根据动量守恒定律:
2mv10=mv1
用E1表示最大弹性势能,由能量守恒有
| 1 |
| 2 |
| v | 2 10 |
| 1 |
| 2 |
| v | 2 10 |
| 1 |
| 2 |
| v | 2 1 |
解得
E1=
| 1 |
| 4 |
振子2 被碰撞后瞬间,左端小球速度为
|
|
同样分析可得
E2=E3=…EN-1=0
振子N被碰撞后瞬间,左端小球速度 v′N-1=
|
2mvN0=mv?N-1
用EN表示最大弹性势能,根据能量守恒,有
| 1 |
| 2 |
| v | 2 N0 |
| 1 |
| 2 |
| v | 2 N0 |
| 1 |
| 2 |
| v | 2 N-1 |
解得
EN=
| 1 |
| 4 |
故所有可能的碰撞都发生后第一个弹簧振子的最大弹性势能为
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题关键在于第一小问中弹簧振子的运动,其系统重心向右匀速,两球速度交替增加与减小,当左侧球速度为零时右侧球速度最大,当右侧球速度为零时左侧球速度最大;同时第二问中要能够找到循环的过程和两个非循环的过程.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目