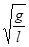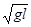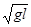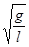题目内容
奥运会单杠比赛中有一个“单臂大回环”动作,难度系数非常大.假设运动员质量为m,单臂抓杠身体下垂时,手掌到人体重心的距离为l,在运动员单臂回转从顶点倒立(已知此时速度为0)转动至最低点的过程中(可将人视作质量集中于重心的质点,且不考虑手掌与单杠间的摩擦力,重力加速度为g).下列分析不正确的有( )
分析:(1)运动员单臂回转从顶点倒立(已知此时速度为0)转动至最低点的过程中做圆周运动,根据动能定理可以求出最低点的速度;
(2)在最低点,手臂拉力和重力的合力提供向心力,根据向心力公式即可求出合力,再根据牛顿第二定律即可求出加速度;
(3)根据向心力公式中的角速度公式即可求出最低点的角速度.
(2)在最低点,手臂拉力和重力的合力提供向心力,根据向心力公式即可求出合力,再根据牛顿第二定律即可求出加速度;
(3)根据向心力公式中的角速度公式即可求出最低点的角速度.
解答:解:运动员单臂回转从顶点倒立(已知此时速度为0)转动至最低点的过程中,根据动能定理得:
mv2-0=mg?2L
解得:v=
在最低点有:
F-mg=m
=ma
F=5mg,a=4g
根据mω2L=ma得;
ω=2
由此可知ABD结论正确,C错误
故选C.
| 1 |
| 2 |
解得:v=
| 2gL |
在最低点有:
F-mg=m
| v2 |
| L |
F=5mg,a=4g
根据mω2L=ma得;
ω=2
|
由此可知ABD结论正确,C错误
故选C.
点评:该题是圆周运动向心力公式的直接应用,难度适中,属于中档题.

练习册系列答案
相关题目