题目内容
6.某海事搜救直升机在夜间进行海上援救,直升机悬停在离海面高为H处,用探照灯搜索海面,当光柱锁定一个随海水漂流的遇险者时,探照灯光柱在竖直平面内转动,此时仪器显示探照灯转动的角速度为ω,搜救船测得海水流速为v,则遇险者到直升机的水平距离为( )| A. | $\frac{v}{ω}$-H | B. | $\sqrt{\frac{ω{H}^{3}}{v-ωH}}$ | C. | $\sqrt{\frac{H}{ω}-{H}^{2}}$ | D. | $\sqrt{(\frac{v}{ω})^{2}-{H}^{2}}$ |
分析 根据分运动与合运动的关系,结合矢量法则,及几何关系,即可求解.
解答  解:遇险者的漂流速度v可分解为此时光柱转动的线速度v1和沿光柱延伸的速度v2,
解:遇险者的漂流速度v可分解为此时光柱转动的线速度v1和沿光柱延伸的速度v2,
其中v1=ωr=$\frac{ωH}{cosθ}$,因此cos$θ=\frac{{v}_{1}}{v}$=$\frac{ωH}{vcosθ}$,
${cos^2}θ=\frac{H^2}{{{H^2}+{s^2}}}$,
解得$s=\sqrt{\frac{{\user1{v}H}}{ω}-{H^2}}$$s=\sqrt{\frac{vH}{ω}-{H}^{2}}$,故C正确,ABD错误;
故选:C.
点评 考查运动的分解与合成,掌握分运动与合运动的等时性,及如何确定分运动是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.汽车在水平路面上做匀速运动,发动机输出的功率为P,速度为v,当汽车上坡时( )
| A. | 如果输出的功率不变,则应减小速度 | |
| B. | 如果输出的功率不变,则应增大速度 | |
| C. | 如果保持速度不变,则应减小输出功率 | |
| D. | 如果保持速度不变,则应增大输出功率 |
17.电磁波在日常生活和生产中已经被大量应用了.下面正确的是( )
| A. | 手机通话使用的无线电波,波长比可见光长 | |
| B. | 银行的验钞机和家用电器的遥控器发出的光都是紫外线 | |
| C. | 微波炉能快速加热食物是利用红外线具有显著的热效应 | |
| D. | 机场、车站用来检查旅客行李包的透视仪是利用X射线的穿透本领 |
9.质量为m的物体从高h处自由落下(不计空气阻力),当它下落到高度为$\frac{3}{4}$h处时动能为( )
| A. | mgh | B. | $\frac{1}{4}$mgh | C. | $\frac{1}{2}$mgh | D. | $\frac{3}{4}$mgh |

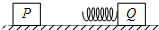 如图所示,位于光滑水平桌面上的小滑块P和Q均可视为质点,质量均为m,Q与轻质弹簧相连并处于静止状态,P以初速度v向Q运动并与弹簧发生作用.求运动过程中弹簧的最大弹性势能及此时两滑块的速度大小.
如图所示,位于光滑水平桌面上的小滑块P和Q均可视为质点,质量均为m,Q与轻质弹簧相连并处于静止状态,P以初速度v向Q运动并与弹簧发生作用.求运动过程中弹簧的最大弹性势能及此时两滑块的速度大小.
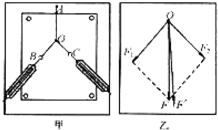 “验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.