题目内容
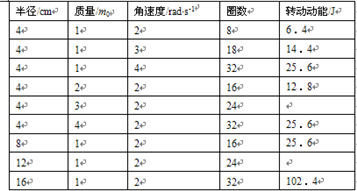
某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关,他以圆型砂轮为研究对象,研究其转动动能与其质量、半径、角速度等的具体关系.如图所示,砂轮由动力带动匀速旋转,测得其角速度为ω,然后让砂轮脱离动力,用一把弹性尺子与砂轮接触使砂轮慢慢停下,设尺和砂轮间的摩擦力恒为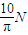 ,不计转轴的质量及其与支架间的摩擦.分别取不同质量、不同半径的砂轮,使其以不同的角速度旋转进行实验,最后得到的数据如表所示:
,不计转轴的质量及其与支架间的摩擦.分别取不同质量、不同半径的砂轮,使其以不同的角速度旋转进行实验,最后得到的数据如表所示: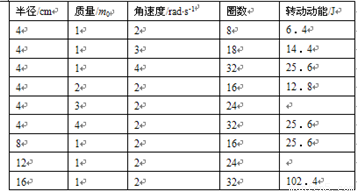
(1)该同学计算了其中五次砂轮的转动动能,请你计算其他两次次砂轮的转动动能并填在上面表格的空白处.
(2)由上述数据推导出该砂轮的转动动能Ek与质量m、角速度ω、半径r的关系式______.
(3)以上实验运用了物理学中的一个重要的思维方法是:______.
【答案】分析:根据第一、二、三组数据,半径、质量相同,角速度不同,分析转动动能,发现转动动能与角速度的二次方成正比.根据第一、四组数据,半径、角速度相同,质量不同,分析转动动能,发现转动动能与质量成正比.根据第一、七组数据,或第七、九组数据,质量、角速度相同,半径不同,分析转动动能,发现转动动能与半径的二次方成正比.最终得出转动动能与质量成正比、与半径和角速度的二次方成正比,表达式为:EK=kmω2r2(k为比例系数).从而得出两空格的转动动能.在处理以上数据时,控制几个量不变,改变一个量,从而得出它们的关系,在物理上称为控制变量法.
解答:解:(1)根据第一、二、三组数据,半径、质量相同,角速度不同,发现角速度变为原来的2倍,转动动能变为原来的4倍,角速度变为原来的 倍,转动动能变为原来的
倍,转动动能变为原来的 倍,可知转动动能与角速度的二次方成正比.根据第一、四组数据,半径、角速度相同,质量不同,发现质量变为原来的2倍,转动动能变为原来的2倍,可知转动动能与质量成正比.根据第七、九组数据,质量、角速度相同,半径不同,发现半径变为原来的2倍,转动动能变为原来的4倍,可知转动动能与半径的二次方成正比,综上所述,转动动能与质量成正比、与半径和角速度的二次方成正比,表达式为:EK=kmω2r2(k为比例系数).第五组数据中,半径和角速度与第一组数据中相同,质量变为原来的3倍,所以转动动能为原来的3倍,故答案为:19.2J.第八组数据中,质量和角速度与第一组数据中相同,半径变为原来的3倍,所以转动动能为原来的9倍,故答案为:57.6J.
倍,可知转动动能与角速度的二次方成正比.根据第一、四组数据,半径、角速度相同,质量不同,发现质量变为原来的2倍,转动动能变为原来的2倍,可知转动动能与质量成正比.根据第七、九组数据,质量、角速度相同,半径不同,发现半径变为原来的2倍,转动动能变为原来的4倍,可知转动动能与半径的二次方成正比,综上所述,转动动能与质量成正比、与半径和角速度的二次方成正比,表达式为:EK=kmω2r2(k为比例系数).第五组数据中,半径和角速度与第一组数据中相同,质量变为原来的3倍,所以转动动能为原来的3倍,故答案为:19.2J.第八组数据中,质量和角速度与第一组数据中相同,半径变为原来的3倍,所以转动动能为原来的9倍,故答案为:57.6J.
(2)表达式为:EK=kmω2r2(k为比例系数).
(3)分析的过程中总要控制一些量不变,故答案为:控制变量法.
点评:研究某一物理量与几个量的关系时,必须控制其它量不变,去改变一个量,找出它们的关系,然后再控制其它量不变,再去改变一个量,再找出关系,依次类推,最终就能找出这一物理量与其他量的关系.
解答:解:(1)根据第一、二、三组数据,半径、质量相同,角速度不同,发现角速度变为原来的2倍,转动动能变为原来的4倍,角速度变为原来的
 倍,转动动能变为原来的
倍,转动动能变为原来的 倍,可知转动动能与角速度的二次方成正比.根据第一、四组数据,半径、角速度相同,质量不同,发现质量变为原来的2倍,转动动能变为原来的2倍,可知转动动能与质量成正比.根据第七、九组数据,质量、角速度相同,半径不同,发现半径变为原来的2倍,转动动能变为原来的4倍,可知转动动能与半径的二次方成正比,综上所述,转动动能与质量成正比、与半径和角速度的二次方成正比,表达式为:EK=kmω2r2(k为比例系数).第五组数据中,半径和角速度与第一组数据中相同,质量变为原来的3倍,所以转动动能为原来的3倍,故答案为:19.2J.第八组数据中,质量和角速度与第一组数据中相同,半径变为原来的3倍,所以转动动能为原来的9倍,故答案为:57.6J.
倍,可知转动动能与角速度的二次方成正比.根据第一、四组数据,半径、角速度相同,质量不同,发现质量变为原来的2倍,转动动能变为原来的2倍,可知转动动能与质量成正比.根据第七、九组数据,质量、角速度相同,半径不同,发现半径变为原来的2倍,转动动能变为原来的4倍,可知转动动能与半径的二次方成正比,综上所述,转动动能与质量成正比、与半径和角速度的二次方成正比,表达式为:EK=kmω2r2(k为比例系数).第五组数据中,半径和角速度与第一组数据中相同,质量变为原来的3倍,所以转动动能为原来的3倍,故答案为:19.2J.第八组数据中,质量和角速度与第一组数据中相同,半径变为原来的3倍,所以转动动能为原来的9倍,故答案为:57.6J.(2)表达式为:EK=kmω2r2(k为比例系数).
(3)分析的过程中总要控制一些量不变,故答案为:控制变量法.
点评:研究某一物理量与几个量的关系时,必须控制其它量不变,去改变一个量,找出它们的关系,然后再控制其它量不变,再去改变一个量,再找出关系,依次类推,最终就能找出这一物理量与其他量的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2011?上海二模)某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关,他以圆型砂轮为研究对象,研究其转动动能与其质量、半径、角速度等的具体关系.如图所示,砂轮由动力带动匀速旋转,测得其角速度为ω,然后让砂轮脱离动力,用一把弹性尺子与砂轮接触使砂轮慢慢停下,设尺和砂轮间的摩擦力恒为
(2011?上海二模)某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关,他以圆型砂轮为研究对象,研究其转动动能与其质量、半径、角速度等的具体关系.如图所示,砂轮由动力带动匀速旋转,测得其角速度为ω,然后让砂轮脱离动力,用一把弹性尺子与砂轮接触使砂轮慢慢停下,设尺和砂轮间的摩擦力恒为