题目内容
【题目】轻质弹簧原长为2l，将弹簧竖直放置在地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为l．现将该弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接．AB是长度为5l的水平轨道，B端与半径为l的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图所示．物块P与AB间的动摩擦因数μ=0.5．用外力推动物块P，将弹簧压缩至长度l，然后释放，P开始沿轨道运动，重力加速度大小为g．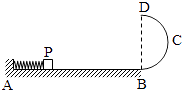
（1）若P的质量为m，求P到达B点时速度的大小，以及它离开圆轨道后落回到AB上的位置与B点间的距离；
（2）若P能滑上圆轨道，且仍能沿圆轨道滑下，求P的质量的取值范围．
【答案】
（1）解：将弹簧竖直放置在地面上，物体下落压缩弹簧时，由系统的机械能守恒得
Ep=5mgl
如图，根据能量守恒定律得
Ep=μmg4l+ 
联立解得 vB= 
物体P从B到D的过程，由机械能守恒定律得
mg2l+ 
=
解得 vD= 
＞ 
所以物体P能到达D点，且物体P离开D点后做平抛运动，则有
2l= 
x=vDt
解得 x=2 
l
即落地点与B点间的距离为2 l
答：P到达B点时速度的大小是 ，它离开圆轨道后落回到AB上的位置与B点间的距离是2 l
（2）解：P刚好过B点，有：Ep=μm1g4l，解得 m1= 
m
P最多到C而不脱轨，则有 Ep=μm2g4l+m2gl，解得 m2= 
m
所以满足条件的P的质量的取值范围为： m≤mP＜ m
答：P的质量的取值范围为： m≤mP＜ m
【解析】（1）先研究弹簧竖直的情况，根据系统的机械能守恒求出弹簧最大的弹性势能．弹簧如图放置时，由于弹簧的压缩量等于竖直放置时的压缩量，两种情况弹簧的弹性势能相等．由能量守恒定律求出物体P滑到B点时的速度，由机械能守恒定律求出物体P到达D点的速度．物体P离开D点后做平抛运动，由平抛运动的规律求水平距离．（2）P能滑上圆轨道，且仍能沿圆轨道滑下，能上升的最高点为C，根据能量守恒定律列式和临界条件求解．
