题目内容
17．
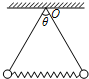如图所示，两完全相同的小球，质量均为m，用两根等长的细线悬挂在O点，两球之间夹着一根劲度系数为k的轻弹簧．系统处于静止状态时，弹簧位于水平方向，两根细线之间的夹角为θ=60°，重力加速度为g．求弹簧的形变量x．
分析 对A球受力分析，然后根据平衡条件并运用合成法得到弹簧的弹力，最后根据胡克定律得到弹簧的压缩量．
解答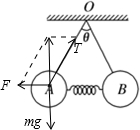 
解：对球A受力分析，受重力mg、拉力T、弹簧的弹力F，如图
由平衡条件得轻弹簧作用力大小为：F=mgtan30°=$\frac{\sqrt{3}}{3}$mg
由胡克定律 F=kx 得：x=$\frac{\sqrt{3}mg}{3k}$
答：弹簧的形变量x是$\frac{\sqrt{3}mg}{3k}$．
点评 本题关键是对小球受力分析，然后根据共点力平衡条件并运用合成法求解出弹力，最后根据胡克定律求解出弹簧的压缩量．
练习册系列答案
阅读快车系列答案
相关题目
7．
如图表示两个质点的速度--时间图象．某同学从图象得出以下结论：①两个质点的速度方向相反；②两个质点的加速度方向相反；③t1时刻两个质点相遇；④t2时刻b质点的加速度不为零．上述结论中正确的是（ ）
如图表示两个质点的速度--时间图象．某同学从图象得出以下结论：①两个质点的速度方向相反；②两个质点的加速度方向相反；③t1时刻两个质点相遇；④t2时刻b质点的加速度不为零．上述结论中正确的是（ ）| A． | ①② | B． | ②④ | C． | ③④ | D． | ②③ |
如图所示，坐标平面第Ⅰ象限内存在大小为E方向水平向左的匀强电场，在第Ⅱ象限内存在大小为B方向垂直纸面向里的匀强磁场．质量为m带电量为q的正电粒子从x轴上的A点以初速度v0垂直x轴射入电场，OA=L，不计重力．求：
5．用一个额定电压为220V的电热水器煮沸一壶水需要ts，如果不考虑煮水时的电热损失和电热丝电阻受温度的影响，那么（ ）
| A． | 当线路电压为110V时，煮沸一壶水需要2ts | |
| B． | 当线路电压为110V时，煮沸一壶水需要4ts | |
| C． | 当线路电压为55V时，煮沸一壶水需要4ts | |
| D． | 当线路电压为55V时，煮沸一壶水需要8ts |
某中学兴趣小组设计了如图所示的装置，利用以下器材：米尺、秒表、轻绳、轻滑轮和总质量为m的若干砝码等，测量两个质量不同的木块A、B的质量mA、mB．已知重力加速度为g．操作步骤如下：
9．
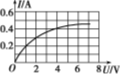如图所示为一个小灯泡的电流与它两端电压的变化关系曲线．若把三个这样的灯泡串联后，接到电压恒定的12V电源上，则此时流过小灯泡的电流和小灯泡的电阻分别为（ ）
如图所示为一个小灯泡的电流与它两端电压的变化关系曲线．若把三个这样的灯泡串联后，接到电压恒定的12V电源上，则此时流过小灯泡的电流和小灯泡的电阻分别为（ ）| A． | I=0.4 A；R=10Ω | B． | I=0.2A；R=60Ω | C． | I=0.4 A；R=30Ω | D． | I=0.6A；R=20Ω |
6．如图所示，地球绕OO′轴自转，则下列正确的是（ ）
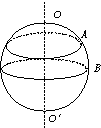
| A． | A、B两点的角速度相等 | B． | A、B两点线速度相等 | ||
| C． | A、B两点的转动半径相同 | D． | A、B两点的转动周期不相同 |
2．若用m表示地球通讯卫星（同步卫星）的质量，h表示它离地面的高度，R0表示地球的半径，a表示距离地球球心r处的做圆周运动的在轨卫星的向心加速度，ω0表示地球自转的角速度，则该通讯卫星所受的地球对它的万有引力的大小F为（ ）
| A． | F=0 | B． | $F=m\frac{R_0^2a}{{{{（{R_0}+h）}^2}}}$ | ||
| C． | $F=m\root{3}{{a{r^2}ω_0^4}}$ | D． | $F=m\frac{r^2}{{{R_0}+h}}a$ |