题目内容
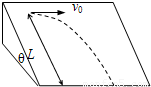
 如右图所示,光滑斜面的倾角为θ,若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出,问小球滑到斜面底端时位移s是多大?末速度vt多大?
如右图所示,光滑斜面的倾角为θ,若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出,问小球滑到斜面底端时位移s是多大?末速度vt多大?某同学对此题的解法为:
平抛出的小球下落高度为Lsinθ,位移为s,则有Lsinθ=
| 1 |
| 2 |
|
由此可求得位移s和末速度vt.
问:你同意上述解法吗?若同意,求出位移s和末速度vt;若不同意,则说明理由并求出你认为正确的结果.
有错误.
错因:小球所做的不是平抛运动,而是类平抛运动.
正解:小球在斜面内的运动情况是:水平方向上,以初速度v0做匀速直线运动;在沿斜面向下的方向上,以加速度a=gsinθ做初速度为零的匀加速直线运动.其运动轨迹为抛物线,称为类平抛运动.
依运动的独立性及等时性有:L=
| 1 |
| 2 |
|
| (v0t)2+L2 |
|
|
∴s=v0
|
|
分析:小球所做的不是平抛运动,而是类平抛运动,所以该同学的解法是错误的.小球的运动可以分解为沿初速度方向的匀速直线运动与垂直于初速度方向的初速度为零的匀加速运动,应用匀速运动与匀变速运动的运动规律可以求出小球的运动时间与水平位移,进而求出末速度.
解答:解:有错误.
错因:小球所做的不是平抛运动,而是类平抛运动.
正解:小球在斜面内的运动情况是:水平方向上,以初速度v0做匀速直线运动;在沿斜面向下的方向上,以加速度a=gsinθ做初速度为零的匀加速直线运动.其运动轨迹为抛物线,称为类平抛运动.
依运动的独立性及等时性有:s=v0t…①,
L=
gsinθ?t2…②,
vt=
…③
解得:s=v0
,
则小球滑到斜面底端时位移是s=
;
末速度为vt=
答:该同学的解法是错误的,小球滑到斜面底端时位移是s=
;末速度vt为 vt=
.
错因:小球所做的不是平抛运动,而是类平抛运动.
正解:小球在斜面内的运动情况是:水平方向上,以初速度v0做匀速直线运动;在沿斜面向下的方向上,以加速度a=gsinθ做初速度为零的匀加速直线运动.其运动轨迹为抛物线,称为类平抛运动.
依运动的独立性及等时性有:s=v0t…①,
L=
| 1 |
| 2 |
vt=
|
解得:s=v0
|
则小球滑到斜面底端时位移是s=
|
末速度为vt=
|
答:该同学的解法是错误的,小球滑到斜面底端时位移是s=
|
|
点评:把小球在斜面上的运动分解为初速度方向的匀速运动与垂直于初速度方向的初速度为零的匀加速度运动,应用运动的合成与分解是正确解题的前提与关键.

练习册系列答案
相关题目
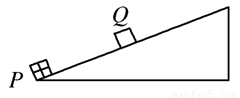
 沿导轨面向上滑出,最后又从滑出处滑回到原处,导轨底端接有电阻R,其余电阻不计。下列说法正确的是
沿导轨面向上滑出,最后又从滑出处滑回到原处,导轨底端接有电阻R,其余电阻不计。下列说法正确的是
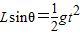 ,s=vt,
,s=vt,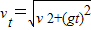 .
.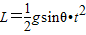
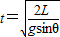
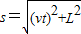 =
=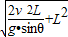
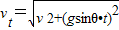
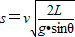
 .
.