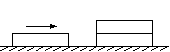题目内容
 如图所示为三块质量均为m,长度均为L的木块1和木块2重叠放置在光滑的水平桌面上,木块3沿光滑水平桌面运动并与叠放在下面的木块2发生碰撞后粘合在一起,如果要求碰后原来叠放在上面的木块1完全移到木块3上,并且不会从木块3上掉下,木块3碰撞前的动能应满足什么条件?设木块之间的动摩擦因数为μ.
如图所示为三块质量均为m,长度均为L的木块1和木块2重叠放置在光滑的水平桌面上,木块3沿光滑水平桌面运动并与叠放在下面的木块2发生碰撞后粘合在一起,如果要求碰后原来叠放在上面的木块1完全移到木块3上,并且不会从木块3上掉下,木块3碰撞前的动能应满足什么条件?设木块之间的动摩擦因数为μ.分析:对3、2组成的系统运用动量守恒求出碰撞后的速度,再对1、2、3组成的系统运用动量守恒求出三者共同的速度,抓住木块1完全移到木块3上,并且不会从木块3上掉下,相对滑动的距离在L-1.5L之间,结合能量守恒定律求出木块3碰撞前的动能.
解答:解:设第3块木块的初速度为υ0,对于3、2两木块的系统,设碰撞后的速度为υ1,据动量守恒定律得:mυ0=2mυ1…①
对于3、2整体与1组成的系统,设共同速度为υ2,则根据动量守恒有:2mυ1=3mυ2…②
(1)第1块木块恰好运动到第3块上,首尾相齐,根据能量守恒有:μmgL=
×2m
-
×3m
…③
由①②③联立方程得:Ek3=6μmgL…④
(2)第1块运动到第3块木块上,恰好不掉下,相对运动的距离为1.5L,据能量守恒定律得:μmg×1.5L=
×2m
-
×3m
…⑤
由①②⑤联立方程得:Ek3=9μmgL
故:6μmgL≤Ek3≤9μmgL
答:木块3碰撞前的动能应满足6μmgL≤Ek3≤9μmgL.
对于3、2整体与1组成的系统,设共同速度为υ2,则根据动量守恒有:2mυ1=3mυ2…②
(1)第1块木块恰好运动到第3块上,首尾相齐,根据能量守恒有:μmgL=
| 1 |
| 2 |
| υ | 2 1 |
| 1 |
| 2 |
| υ | 2 2 |
由①②③联立方程得:Ek3=6μmgL…④
(2)第1块运动到第3块木块上,恰好不掉下,相对运动的距离为1.5L,据能量守恒定律得:μmg×1.5L=
| 1 |
| 2 |
| υ | 2 1 |
| 1 |
| 2 |
| υ | 2 2 |
由①②⑤联立方程得:Ek3=9μmgL
故:6μmgL≤Ek3≤9μmgL
答:木块3碰撞前的动能应满足6μmgL≤Ek3≤9μmgL.
点评:本题综合考查了动量守恒定律和能量守恒定律,关键抓住两个临界状态,结合动量守恒定律和能量守恒定律进行求解.

练习册系列答案
相关题目
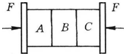
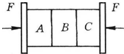 如图所示,三块质量均为m的长方体物体被夹在两竖直木板之间保持静止.图中物体A受到物体B的摩擦力大小为
如图所示,三块质量均为m的长方体物体被夹在两竖直木板之间保持静止.图中物体A受到物体B的摩擦力大小为