题目内容
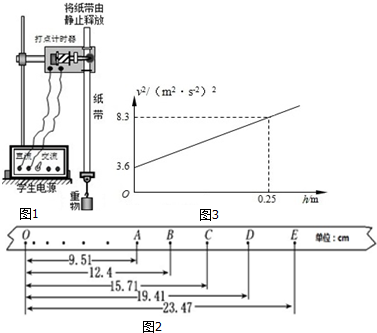
15.如图所示,地面和半圆轨道面均光滑.质量M=1kg、长L=4m的小车放在凹槽地面上,其右端与墙壁距离为s=3m,小车上表面与半圆轨道最低点P的切线相平.现有一质量m=2kg静止的滑块(不计大小),从左侧高为H=3.6m的圆弧形斜劈上滑下,圆弧形斜劈的质量m1=2kg圆弧底部与接触面完美相切滑上小车左端,带动小车向右运动.小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的动摩擦因数μ=0.2,g取10m/s2.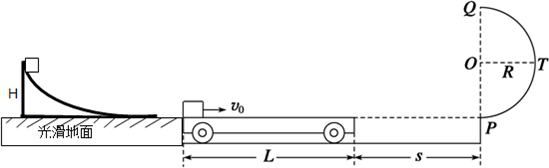
(1)求滑块滑到小车上的初速度?
(2)求小车与墙壁碰撞时的速度;
(3)要滑块能沿半圆轨道运动而不脱离半圆轨道,求半圆轨道的半径R的取值.
分析 (1)滑块在下滑过程中根据动量定理和能量守恒即可求得速度;
(2)滑块滑到小车后滑块做减速运动,小车做加速运动,根据牛顿第二定律和运动学公式即可求得达到的共同速度;
(3)判断出滑块不脱离轨道的条件,即能通过最高点和最高到达T点即可,根据动能定理即可求得轨道半径
解答 解:(1)滑块在下滑的过程中,在水平方向动量守恒,选向右为正方向,故0=mv-m1v1
整个下滑过程中能量守恒$mgH=\frac{1}{2}m{v}^{2}+\frac{1}{2}{{m}_{1}v}_{1}^{2}$
联立解得v=v1=6m./s
(2)滑块滑到小车上后,滑块的加速度为${a}_{1}=\frac{μmg}{m}=μg=2m/{s}^{2}$
小车的加速度为${a}_{2}=\frac{μmg}{M}=\frac{0.2×2×10}{1}m/{s}^{2}=4m/{s}^{2}$
达到共同速度所需时间为t,则v共=v-a1t
v共=a2t
联立解得t=1s,v共=4m/s
1s内各自通过的位移:滑块${x}_{1}=vt-\frac{1}{2}{a}_{1}{t}^{2}=6×1-\frac{1}{2}×2×{1}^{2}m=5m$
小车的位移为${x}_{2}=\frac{1}{2}{a}_{2}{t}^{2}=\frac{1}{2}×4×{1}^{2}m=2m$
△x=x1-x2=5-2m=3m<L=4m,
达到共同速度后小车和滑块一起向右匀速运动,故小车与墙壁碰撞时的速度为4m/s
(3)与墙壁碰撞后,滑块继续做减速运动,到达P点的速度为v′
前进的位移x3=L-△x=1m
故${v}_{P}^{2}{-v}_{共}^{2}=-2{a}_{1}{x}_{3}$
解得vP=2$\sqrt{3}$m/s
当滑块能达到最高点且恰好达到最高点时,根据牛顿第二定律可知mg=$\frac{m{{v}_{Q}}^{2}}{R}$
从P到Q过程由动能定理可得
-2mgR=$\frac{1}{2}{mv}_{Q}^{2}-\frac{1}{2}{mv}_{P}^{2}$
联立解得R=0.24m,故当半径R≤0.24 m不会脱离轨道
当半径增大时,滑块最高到达T也不会脱离,故从P到T根据动能定理可的
$-mgR=0-\frac{1}{2}{mv}_{3}^{2}$
解得R=0.6m,当R≥0.6 m也不会脱离轨道
答:(1)求滑块滑到小车上的初速度为6m/s
(2)求小车与墙壁碰撞时的速度为4m/s;
(3)要滑块能沿半圆轨道运动而不脱离半圆轨道,半圆轨道的半径R的取值为R≤0.24 m或R≥0.6 m
点评 本题主要考查了动量定理和动能定理,以及运动学公式,在第3问中必须判断出临界条件即可利用动能定理求解

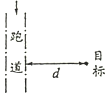 民族运动会上有一个骑射项目,运动员骑在奔驰的马背上,弯弓放箭射击侧向的固定目标,假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭的速度为v2,跑道离固定目标的最近距离为d,如图所示,要想在最短的时间内射中目标,则运动员放箭处离目标的距离和最短时间分别为( )
民族运动会上有一个骑射项目,运动员骑在奔驰的马背上,弯弓放箭射击侧向的固定目标,假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭的速度为v2,跑道离固定目标的最近距离为d,如图所示,要想在最短的时间内射中目标,则运动员放箭处离目标的距离和最短时间分别为( )| A. | $\frac{d{v}_{2}}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ | B. | $\frac{d\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$ | C. | $\frac{d}{{v}_{2}}$ | D. | $\frac{d}{{v}_{1}}$ |
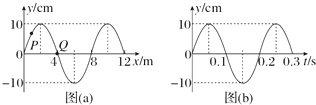
| A. | 在t=0.10s时,质点Q向y轴正方向运动 | |
| B. | 在t=0.25s时,质点P的加速度方向与y轴正方向相同 | |
| C. | 从t=0.10s到t=0.25s,该波沿x轴负方向传播了6m | |
| D. | 从t=0.10s到t=0.25s,质点P通过的路程为30cm |
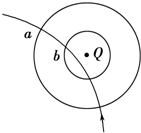 在点电荷Q的电场中,一个电子通过时的轨迹如图实线所示,a、b为两个等势面,则下列判断中正确的是( )
在点电荷Q的电场中,一个电子通过时的轨迹如图实线所示,a、b为两个等势面,则下列判断中正确的是( )| A. | Q为负电荷 | |
| B. | 运动中,电子总是克服电场力做功 | |
| C. | 电子经过两等势面的动能Ekb>Eka | |
| D. | 电子在两等势面上的电势能Epa<Epb |
| A. | 伽利略发现了行星运动的规律 | |
| B. | 牛顿最早指出力不是维持物体运动的原因 | |
| C. | 楞次发现了电流的磁效应,拉开了研究电与磁相互关系的序幕 | |
| D. | 法拉第最出色的成就是电磁感应的发现和场的概念的提出 |
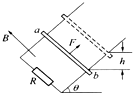 两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻可忽略不计.斜面处在匀强磁场中,磁场方向垂直于斜面向上.质量为m、电阻可不计的金属棒ab,在沿着斜面与棒垂直的恒力F作用下沿导轨匀速上滑,并上升h高度.如图所示,在这过程中( )
两根光滑的金属导轨,平行放置在倾角为θ的斜面上,导轨的左端接有电阻R,导轨自身的电阻可忽略不计.斜面处在匀强磁场中,磁场方向垂直于斜面向上.质量为m、电阻可不计的金属棒ab,在沿着斜面与棒垂直的恒力F作用下沿导轨匀速上滑,并上升h高度.如图所示,在这过程中( )| A. | 作用于金属棒上的各个力的合力所做的功等于零 | |
| B. | 作用于金属棒上的各个力的合力所做的功等于mgh与电阻R上发出的焦耳热之和 | |
| C. | 恒力F与安培力的合力所做的功等于零 | |
| D. | 恒力F与重力的合力所做的功等于电阻R上发出的焦耳热 |