题目内容
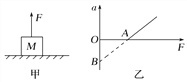
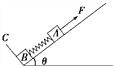
【题目】如图所示，在倾角θ＝30°的光滑斜面上有两个用轻质弹簧相连接的物块A，B，它们的质量均为m，弹簧的劲度系数为k，C为一固定挡板，系统处于静止状态．现开始用一沿斜面方向的力F拉物块A使之以加速度a向上做匀加速运动，当物块B刚要离开C时力F的大小恰为2mg.则( )
A. 物块B刚要离开C时B的加速度为0
B. 加速度a＝
g
C. 无法计算出加速度a
D. 从F开始作用到B刚要离开C，A的位移为
【答案】AD
【解析】试题分析：当物块B刚要离开C时，对挡板的压力为零，根据平衡条件求出此时弹簧的弹力，结合胡克定律求出弹簧的形变量．对A，根据牛顿第二定律求出物块A的加速度．弹簧开始处于压缩，根据平衡求出压缩量的大小，抓住A的位移等于弹簧的形变量求出物块A的位移．
物块B刚要离开C时，B和挡板之间没有力的作用，即弹簧的拉力正好等于B的重力沿斜面向下的分力，所以此时B的合力为零，加速度为零，A正确；物块B刚要离开C时，
弹簧的弹力
，所以对A分析，受到弹簧沿斜面向下的拉力，和重力沿斜面向下的分力以及F的作用，根据牛顿第二定律可得
，解得
，BC错误；未施加F之前，弹簧处于压缩状态，对A分析有
，当物块B刚要离开C时弹簧处于拉伸状态，对B分析有
，故A上升的位移为
，D正确．
走进文言文系列答案
【题目】为了测定干电池的电动势和内阻，现有下列器材：
A．干电池一节
B．电压表v1（0-15V，内阻约为15KΩ）
C．电压表v2（0-3V，内阻约为3KΩ）
D．电流表A1（0-3A，内阻约为2Ω）
E．电流表A2（0-0.6A，内阻约为10Ω）
F．电流表G（满偏电流3mA，内阻Rg=10Ω）
G．变压器
H．滑动变阻器（0-1000Ω）
I．滑动变阻器（0-20Ω）
J．开关、导线
（1）用电流表和电压表测量干电池的电动势和内电阻，应选用的滑动变阻器是 ______ ，电流表 ______ ，电压表 ______ （用代号回答）
（2）根据实验要求，用笔画线代替导线在实物图甲上连线．
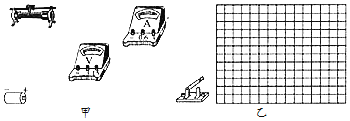
（3）某次实验记录如下：
组别 | 1 | 2 | 3 | 4 | 5 | 6 |
电流I/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.50 | 0.57 |
电压U/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.10 | 1.05 |
根据表中数据在坐标图乙上画出U-I图线，由图可求得E= ______ V，r= ______ Ω．
（4）用你设计的电路做实验，测得的电动势与电池电动势的真实值相比 ______ （填“偏大”“偏小”或“相等”）．
