Question

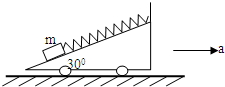如图所示，在小车的倾角为30⁰的光滑斜面上，用劲度系数k=500N/m的弹簧连接一质量为m=1kg的物体．
（1）当小车以

3

m/s2的加速度运动时，m与斜面保持相对静止，求弹簧伸长的长度．
（2）若使物体m对斜面无压力，小车加速度必须多大？
（3）若使弹簧保持原长，小车加速度大小、方向如何？

Answer 1

分析：（1）对小滑块受力分析，受重力、支持力和拉力；再根据牛顿第二定律求出合力的大小和方向，然后运用正交分解法列式求解；
（2）小滑块对斜面体没有压力，则斜面体对小滑块也没有支持力，小滑块受到重力和拉力，物体的加速度水平向右，故合力水平向右，运用平行四边形定则求解合力，再根据牛顿第二定律求解加速度；
（3）弹簧保持原长，弹力为零，小滑块受到重力和支持力，物体沿水平方向运动，加速度水平向左，合力水平向左，运用平行四边形定则求解合力，再根据牛顿第二定律求解加速度的大小．

解答：解：（1）对小滑块受力分析，受重力、支持力和拉力，如图

加速度水平向右，故合力水平向右，将各个力和加速度都沿斜面方向和垂直斜面方向正交分解，由牛顿第二定律，得到
F-mg?sin30°=ma?cos30°
mg?cos30°-F_N=ma?sin30°
解得
F=mg?sin30°+ma?cos30°=6.5N
根据胡克定律，有
F=kx
代入数据得到
x=0.013m=1.3cm
即此时当小车以

3

m/s2的加速度运动时，弹簧伸长的长度为1.3cm．
（2）小滑块对斜面体没有压力，则斜面体对小滑块也没有支持力，小滑块受到重力和拉力，物体的加速度水平向右，故合力水平向右，运用平行四边形定则，如图

由几何关系得到
F_合=

mg

tan30°

=

1×10

3 3

=10

3

N
根据牛顿第二定律，得到
a=

F合

m

=10

3

m/s²
即若使物体m对斜面无压力，小车加速度必须为10

3

m/s²．
（3）弹簧保持原长，弹力为零，小滑块受到重力和支持力，物体沿水平方向运动，加速度水平向左，合力水平向左，运用平行四边形定则，如图

根据几何关系，有
F_合=mg?tan30°
根据牛顿第二定律，有
F_合=ma
故a=g?tan30°=

10

3

3

m/s²
即小车加速度大小为

10

3

3

m/s²、方向水平向左．

点评：本题关键对小滑块受力分析后，根据牛顿第二定律，运用正交分解法或合成法列式求解．