题目内容
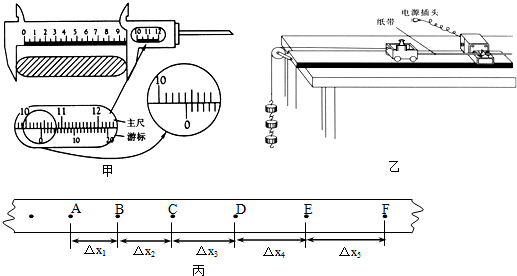
(1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.这种游标卡尺测量长度可以精确到 mm,现用它测量一工件的长度,如图甲所示,图示的读数是 mm;
(2)科学规律的发现离不开科学探究,而科学探究可以分为理论探究和实验探究.下面我们用第二种方法探究恒力做功和物体动能变化间的关系.
①某同学的实验方案如图乙所示,他想用钩码的重力(图中用到的钩码和砝码的重力已知)表示小车受到的合外力,为了减小这种做法带来的实验误差,你认为在实验中还应该采取的两项措施是:
a. ;
b. ;
②如图丙所示是某次实验中得到的一条纸带,其中A、B、C、D、E、F叫计数点,相邻计数点间的时间间隔为T.则打C点时小车的速度为 ;要验证合外力的功与动能变化间的关系,除位移、速度外,还要测出的物理量有 .
③这个实验所探究的规律实际上就是我们所学过的 定理,它的表达式是 .

(2)科学规律的发现离不开科学探究,而科学探究可以分为理论探究和实验探究.下面我们用第二种方法探究恒力做功和物体动能变化间的关系.
①某同学的实验方案如图乙所示,他想用钩码的重力(图中用到的钩码和砝码的重力已知)表示小车受到的合外力,为了减小这种做法带来的实验误差,你认为在实验中还应该采取的两项措施是:
a.
b.
②如图丙所示是某次实验中得到的一条纸带,其中A、B、C、D、E、F叫计数点,相邻计数点间的时间间隔为T.则打C点时小车的速度为
③这个实验所探究的规律实际上就是我们所学过的
分析:(1)游标尺的精确度=
mm,游标卡尺读数的方法是主尺读数加上游标读数,不需估读.
(2)①小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;其次:设小车加速度为a,则:绳上的力为F=Ma,对钩码来说:mg-F=ma,即:mg=(M+m)a,如果用钩码的重力表示小车受到的合外力,则Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量.
②匀变速直线运动中时间中点的速度等该过程中的平均速度,由此可以求出某点的瞬时速度,根据功能关系写出需要验证的表达式,由此可知需要测量的物理量.
③根据动能定理的表达式得出正确结果.
| 1 |
| 等分刻度数 |
(2)①小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;其次:设小车加速度为a,则:绳上的力为F=Ma,对钩码来说:mg-F=ma,即:mg=(M+m)a,如果用钩码的重力表示小车受到的合外力,则Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量.
②匀变速直线运动中时间中点的速度等该过程中的平均速度,由此可以求出某点的瞬时速度,根据功能关系写出需要验证的表达式,由此可知需要测量的物理量.
③根据动能定理的表达式得出正确结果.
解答:解:(1)游标尺上有20个等分刻度,因此精确度为:
mm=0.05mm;
游标卡尺的主尺读数为104mm,游标尺上第1个刻度与主尺上某一刻度对齐,故其读数为1×0.05mm=0.05mm,所以最终读数为:104mm+0.05mm=104.05mm.
(2)①小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;
其次:设小车质量M,钩码质量m,整体的加速度为a,绳上的拉力为F,则:对小车有:F=Ma;对钩码有:mg-F=ma,即:mg=(M+m)a;
如果用钩码的重力表示小车受到的合外力,则要求:Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量,这样两者才能近似相等.
②C是BD的中间时刻,所以C点的速度就等于BD过程中的平均速度:
vC=
验证合外力的功与动能变化间的关系的原理:mgx=
Mv2,需要测量的物理量有:钩码质量m,小车的质量M,位移x,速度v.
③根据动能的表达式可知:W合=
m
-
m
,因此这个实验所探究的规律实际上就是我们所学的动能定理.
故答案为:(1)0.05;104.05.
(2)①平衡摩擦力,钩码的质量远小于小车的总质量;②钩码质量m,小车的质量M,③动能,W合=
m
-
m
.
| 1 |
| 20 |
游标卡尺的主尺读数为104mm,游标尺上第1个刻度与主尺上某一刻度对齐,故其读数为1×0.05mm=0.05mm,所以最终读数为:104mm+0.05mm=104.05mm.
(2)①小车在水平方向上受绳的拉力和摩擦力,想用钩码的重力表示小车受到的合外力,首先需要平衡摩擦力;
其次:设小车质量M,钩码质量m,整体的加速度为a,绳上的拉力为F,则:对小车有:F=Ma;对钩码有:mg-F=ma,即:mg=(M+m)a;
如果用钩码的重力表示小车受到的合外力,则要求:Ma=(M+m)a,必须要满足钩码的质量远小于小车的总质量,这样两者才能近似相等.
②C是BD的中间时刻,所以C点的速度就等于BD过程中的平均速度:
vC=
| △x2+△x3 |
| 2T |
验证合外力的功与动能变化间的关系的原理:mgx=
| 1 |
| 2 |
③根据动能的表达式可知:W合=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 0 |
故答案为:(1)0.05;104.05.
(2)①平衡摩擦力,钩码的质量远小于小车的总质量;②钩码质量m,小车的质量M,③动能,W合=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 0 |
点评:要明确此题在验证合外力的功与动能变化间的关系中用到的原理,围绕原理,记忆需要测量的物理量及实验时的注意事项.

练习册系列答案
相关题目