��Ŀ����
����Ŀ����һ�ξ�Ԯ�У�һ������ͣ��һСɽ�µף�ͻȻ˾�������ھ��µ�240m��ɽ�´�һ��ʯ��8m/s�ij��ٶ�0.4m/s2�ļ��ٶ��ȼ��ٹ��£���ʯ�����µ����ʲ��䣬��ˮƽ����˶����Խ��ƿ��ɼ��ٶȴ�СΪ0.2m/s2���ȼ���ֱ���˶���˾�����������2s��������������������0.5m/s2�ļ��ٶ�һֱ���ȼ���ֱ���˶� ����ͼ��ʾ������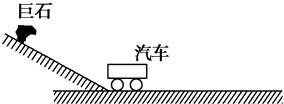
��1����ʯ�����µ�ʱ������ʷֱ��Ƕ��٣�
��2������˾���ܷ�ȫ���գ�
���𰸡�
��1��
�⣺���ʯ�����µ�ʱ��Ϊt1������Ϊv1�����У�
x=v0t1+ ![]() a1t2
a1t2
v1=v0+a1t1
������ֵ�ã�t1=20 s��v1=16 m/s
��2��
�⣺��������18 sʱ���ڷ�����λ��Ϊ��
x1= ![]() a��t��2��2=
a��t��2��2= ![]() =81 m
=81 m
�ٶ�Ϊ��v2=a��t��2��=0.5��18m/s=9 m/s
���پ���ʱ��t�䣬��ʯ�������ٶ���ȣ����У�
v1��a1t��=v2+at��
������ֵ�ã�t��=10 s
���Դ˾�ʯ��ˮƽ���Ϸ�����λ��Ϊ��
s1=v1t�䩁 ![]() a1t��2=
a1t��2= ![]() =150 m
=150 m
���������������
s2= ![]() a��t��2+t�䣩2=
a��t��2+t�䣩2= ![]() =196 m��s1
=196 m��s1
���������ܰ�ȫ����
����������1�������ȱ���ֱ���˶���λ��ʱ�乫ʽ�ó���ʯ�����µ�ʱ�䣬����ٶ�ʱ�乫ʽ�����ʯ�����µ��ٶȴ�С����2�������ٶ�ʱ�乫ʽ�����ʯ�����µ�ʱ�������ٶȣ�ץס��ʯ�������ٶ���ȣ���������˶���ʱ�䣬������ߵ�λ�ƹ�ϵ�ж��Ƿ�ȫ���գ�

 ����������������ϵ�д�
����������������ϵ�д�