题目内容
【题目】如图所示，在屏蔽装置底部中心位置O点放一医用放射源，可通过细缝沿扇形区域向外辐射速率为v=3.2×106m的α粒子．已知屏蔽装置宽AB=9cm、缝长AD=18cm，α粒子的质量m=6.64×10﹣27kg，电量q=3.2×10﹣19C．若在屏蔽装置右侧条形区域内加一匀强磁场来隔离辐射，磁感应强度B=0.332T，方向垂直于纸面向里，整个装置放于真空环境中．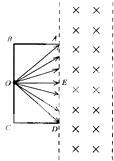
（1）若所有的α粒子均不能从条形磁场隔离区的右侧穿出，则磁场的宽度d至少是多少？
（2）若条形磁场的宽度d=20cm，则射出屏蔽装置的α粒子在磁场中运动的最长时间和最短时间各是多少？（结果保留2位有效数字）
【答案】
（1）
解：由题意：AB=9cm，AD=18cm，
由几何知识可得：∠BAO=∠ODC=45° ①
所有α粒子在磁场中做匀速圆周运动的半径相同，设为R，
由牛顿第二定律得：qvB=m 
②
解得：R=0.2m=20cm ③
由几何知识可知，若条形磁场区域的右边界与沿OD方向进入磁场的α粒子的轨迹相切，
则所有的α粒子均不能从条形磁场隔离区右侧穿出，如图所示：
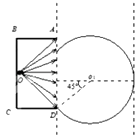
此时磁场宽度为d0，由几何知识得：
d0=R+Rcos45°，解得：d0=（20+10 
）m=0.34m
（2）
解：设α粒子在磁场内做匀速圆周运动的周期为T，
则周期：T= 
= 
×10﹣6s，
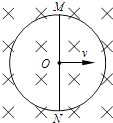
设速度方向垂直于AD进入磁场区域的α粒子的入射点为E，如图所示：
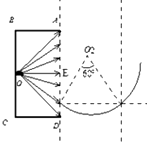
因为磁场宽度d=20cm＜d0，且R=20cm，
则在∠EOD间射出进入磁场区域的α粒子均能穿出磁场右边界，
在∠EOA间出射进入磁场区域的α粒子均不能穿出磁场右边界，
所以沿OE方向进入磁场区域的α粒子运动轨迹与磁场右边界相切，在磁场中运动时间最长，
设在磁场中运动的最长时间为tmax，则：
tmax= 
T≈2×10﹣7s；
若α粒子在磁场中做匀速圆周运动对应的圆弧轨迹的弦最短，
则α粒子穿过磁场时间最短，最短弦长为磁场宽度为d，
设在磁场中运动的最短时间为tmin，由图示可知，R=d，
圆弧对应的圆心角为60°，
则tmin= 
T≈6.5×10﹣8s
【解析】（1）由牛顿第二定律求出粒子运动轨迹，由几何知识可以求出磁场宽度；（2）分析清楚粒子运动轨迹，根据粒子做圆周运动的周期公式可以求出粒子的运动时间．
【考点精析】认真审题，首先需要了解匀速圆周运动(匀速圆周运动线速度的大小恒定，角速度、周期和频率都是恒定不变的，向心加速度和向心力的大小也都是恒定不变的，是速度大小不变而速度方向时刻在变的变速曲线运动)，还要掌握洛伦兹力(洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功)的相关知识才是答题的关键．
