Question

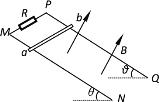
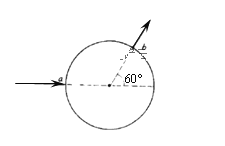
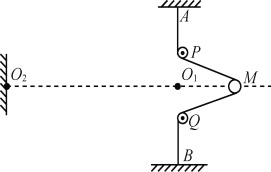
【题目】某打靶游戏的简化示意图如图所示．整个装置置于水平地面上．两根原长等于AP(或BQ)的完全相同轻质弹性绳，一端分别固定在水平地面上A、B两点，另一端系在一起，P、Q为水平地面上的定滑轮，将质量为m＝0.4kg的弹丸置于O1，用弹丸向右推弹性绳的节点到距离O1为r＝0.4 m的M点，由静止释放弹丸，弹丸沿MO1在地面上滑行恰能运动至靶心O2处，已知O1O2的距离s＝0.4m，弹丸与地面动摩擦因数为μ＝0.5，重力加速度g取10 m/s2.求：

(1)弹丸到达O1位置时的速度大小；

(2)弹性绳的释放弹性势能Ep；

(3)每根弹性绳的劲度系数k和弹丸的最大速度vm.

Answer 1

【答案】(1) v＝2m/s (2)Ep＝1.6J (3)，

【解析】

运用动能定理研究从O1运动到O2的过程，列出等式求解速度；弹簧的弹力做的功量度弹簧弹性势能的变化．弹力关于形变量线性变化，可以用平均力乘以位移表示弹力做的功.

(1)弹丸从O1到O2由动能定理：

解得：v＝2m/s

(2)对全过程由系统的能量守恒得Ep＝μmg(s＋r)

所以两弹性绳共释放弹性势能Ep＝1.6J

(3)每根弹性绳的弹力的水平分力Fr＝kΔxcosθ＝kr

解得：

弹丸速度最大时，满足2kr0＝μmg

r0＝0.1m

由动能定理得：

解得：