题目内容
如图所示,一半径为R的圆内有垂直纸面的匀强磁场,磁感应强度为B,CD是该圆一直径。一质量m、电荷量q的带电粒子(不计重力),自A点沿平行CD的方向垂直射入磁场中,恰好从D点飞出磁场,A点到CD的距离为 。则
。则
| A.可判别粒子穿过磁场后做曲线运动 |
| B.可求得粒子在磁场中做圆周运动的轨道半径 |
| C.可求得粒子在磁场中运动时间 |
| D.可求得粒子进入磁场时的速度 |
BCD
解析试题分析:
因不知圆外场的分布情况,带电粒子穿出磁场后不一定做曲线运动,A错;A点到CD的距离 ,∠OAQ=60°,∠DAQ=75°,则∠AQD=30°,偏转角为30°,由此可求出粒子在磁场中运动时间为
,∠OAQ=60°,∠DAQ=75°,则∠AQD=30°,偏转角为30°,由此可求出粒子在磁场中运动时间为 ,C对;根据如图几何关系也可求出粒子做圆周运动的轨道半径,B对;根据时间t可求出粒子的运动周期T,一直轨道半径和周期,就可求出粒子进入磁场时的速度,D对。
,C对;根据如图几何关系也可求出粒子做圆周运动的轨道半径,B对;根据时间t可求出粒子的运动周期T,一直轨道半径和周期,就可求出粒子进入磁场时的速度,D对。
考点:本题考查了粒子在磁场中的运动。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
一个带电粒子,沿垂直于磁场的方向射入一匀强磁场,粒子的一段径迹如图所示,径迹上的每一小段可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图中可以确定 ( )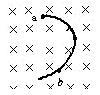
| A.粒子从a到b,带正电 |
| B.粒子从b到a,带正电 |
| C.粒子从a到b,带负电 |
| D.粒子从b到a,带负电 |
关于回旋加速器,下述说法中不正确是
| A.电场的作用是使带电粒子加速,动能增大 |
| B.电场和磁场交替使带电粒子加速 |
| C.磁场的作用是使带电粒子在磁场中回旋,获得多次被加速的机会 |
| D.D形盒的半径越大,射出的带电粒子获得的能量越多 |
下列关于地磁场的描述中正确的是( )
| A.赤道上空的磁感线由北指南 |
| B.通过观察月球磁场和月岩磁性推断,月球内部全部是液态物质 |
| C.磁偏角说明地磁场的南北极与地理的南北极并非完全重合 |
| D.地球南、北极的磁感线和海平面平行 |
根据磁感应强度的定义式 ,下列说法中正确的是( )
,下列说法中正确的是( )
| A.在磁场中某确定位置,B与F成正比,与I、L的乘积成反比 |
| B.一小段通电直导线在空间某处所受磁场力F=0,那么该处的B一定为零 |
| C.一小段通电直导线放在B为零的位置,那么它受到磁场力F也一定为零 |
| D.磁场中某处的B的方向跟电流在该处所受磁场力F的方向相同 |
如图所示,绝缘光滑半圆轨道放在竖直向下的匀强电场中,场强为E,在与环心等高处放有一质量为m,电荷量为+q的小球,由静止开始沿轨道运动,下列说法正确的是( ) 
| A.小球在运动过程中机械能守恒 |
| B.小球经过最低点时机械能最大 |
| C.小球经过环的最低点时对轨道压力为3(mg+qE) |
| D.小球经过环的最低点时对轨道压力为3(mg-qE) |







