题目内容
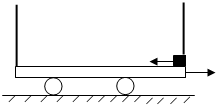 如图,一平行板电容器固定在绝缘小车上,左极板的电势高于右极板的电势,极板间距离为L,小车连同极板的总质量为M,小车在光滑的地平面上正以某一速度向右做匀速直线运动,一质量m=M/3带有正电荷的滑块以跟小车大小相等的初速度从右极板开口处冲入极板间,滑块刚好没能够与左极板相碰(不计滑块与小车的摩擦力)
如图,一平行板电容器固定在绝缘小车上,左极板的电势高于右极板的电势,极板间距离为L,小车连同极板的总质量为M,小车在光滑的地平面上正以某一速度向右做匀速直线运动,一质量m=M/3带有正电荷的滑块以跟小车大小相等的初速度从右极板开口处冲入极板间,滑块刚好没能够与左极板相碰(不计滑块与小车的摩擦力)(1)若小车、滑块的初速度大小均为v0,求系统电势能变化的最大值.
(2)若小车、滑块初速度大小未知,求滑块向左运动到最远处离出发点的位移.
分析:(1)小车、滑块系统动量守恒列出等式,根据能量守恒求解
(2)对系统全过程运用动能定理列出等式,对滑块m速度减为0的过程运用动能定理列出等式求解
(2)对系统全过程运用动能定理列出等式,对滑块m速度减为0的过程运用动能定理列出等式求解
解答:解:(1)设共同速度为v,依动量守恒定律有
Mv0-mv=(M+m)v
得v=
v0
根据能量守恒得系统动能减少等于电势能增量
△E=
mv02+
mv02-
(M+m)v2
得 △E=
=
Mv02
(2)设电场力qE=F
对系统全过程运用动能定理列出等式:
(M+m)v02-
(M+m)v2=FL
对滑块m速度减为0的过程运用动能定理列出等式:
mv02=Fl
由两式解得 l=
答:(1)若小车、滑块的初速度大小均为v0,系统电势能变化的最大值是
Mv02.
(2)若小车、滑块初速度大小未知,滑块向左运动到最远处离出发点的位移是
.
Mv0-mv=(M+m)v
得v=
| 1 |
| 2 |
根据能量守恒得系统动能减少等于电势能增量
△E=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
得 △E=
| 2Mmv02 |
| M+m |
| 1 |
| 2 |
(2)设电场力qE=F
对系统全过程运用动能定理列出等式:
| 1 |
| 2 |
| 1 |
| 2 |
对滑块m速度减为0的过程运用动能定理列出等式:
| 1 |
| 2 |
由两式解得 l=
| L |
| 3 |
答:(1)若小车、滑块的初速度大小均为v0,系统电势能变化的最大值是
| 1 |
| 2 |
(2)若小车、滑块初速度大小未知,滑块向左运动到最远处离出发点的位移是
| L |
| 3 |
点评:该题是一道综合题,综合运用了能量守恒定律、动量守恒定律、动能定理,解决本题的关键熟练这些定理、定律的运用.

练习册系列答案
相关题目
 如图,一平行板电容器充电后与电源断开,从负极板上某处释放一个电子e,设其到达正极板的速度为v1,运动过程中加速度为a1.现将两板间距离增为原来的2倍,再从负极板处释放一电子,设其到达正极板的速度为v2,运动过程中加速度为a2.则有( )
如图,一平行板电容器充电后与电源断开,从负极板上某处释放一个电子e,设其到达正极板的速度为v1,运动过程中加速度为a1.现将两板间距离增为原来的2倍,再从负极板处释放一电子,设其到达正极板的速度为v2,运动过程中加速度为a2.则有( )A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
 如图,一平行板电容器与一电源连接,电源两端的电压保持不变.若使电容器两板间的距离变大,则
如图,一平行板电容器与一电源连接,电源两端的电压保持不变.若使电容器两板间的距离变大,则 如图有一平行板电容器充电后带有等量异种电荷,下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两板板左右水平错开一段很小的距离(极板电量值不变),则下说法中不正确的是( )
如图有一平行板电容器充电后带有等量异种电荷,下极板接地,两极板中央处固定有一个很小的负电荷,现保持两极板间距不变而使两板板左右水平错开一段很小的距离(极板电量值不变),则下说法中不正确的是( ) 如图,一平行板电容器的两个极板竖直放置,在两极板间有一带电小球,小球用一绝缘轻线悬挂于O点.先给电容器缓慢充电,使两级板所带电荷量分别为﹢Q和-Q,此时悬线与竖直方向的夹角为
如图,一平行板电容器的两个极板竖直放置,在两极板间有一带电小球,小球用一绝缘轻线悬挂于O点.先给电容器缓慢充电,使两级板所带电荷量分别为﹢Q和-Q,此时悬线与竖直方向的夹角为