题目内容
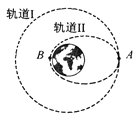
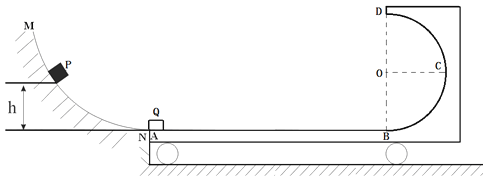
【题目】如图所示,一小车上表面由粗糙的水平部分AB和光滑的半圆弧轨道BCD组成,小车紧靠台阶静止在光滑水平地面上,且左端与光滑圆弧形轨道MN末端等高,圆弧形轨道MN末端水平.一质量为m1=1kg的小物块P从距圆弧形轨道MN末端高为h=1.8m处由静止开始滑下,与静止在小车左端的质量为m2=1kg的小物块Q(可视为质点)发生弹性碰撞(碰后立即将小物块P取走,使之不影响后续物体的运动).若物块Q在半圆弧轨道BCD上经过一次往返运动(运动过程中物块始终不脱离轨道),最终相对小车静止时处在小车水平部分AB的中点。已知AB长为L=4m,小车的质量为M=2kg.取重力加速度g=10m/s2.
(1)求碰撞后瞬间物块Q的速度大小;
(2)求小车上表面的滑动摩擦因数为多少?
(3)求半圆弧轨道BCD的半径至少多大?
【答案】(1)![]() (2)0.2(3)0.4
(2)0.2(3)0.4
【解析】
(1)据机械能守恒求出物块P与物块Q碰撞前的速度,再据碰撞过程是弹性碰撞求出碰撞后瞬间物块Q的速度;(2) 物块Q最终停在小车水平部分AB的中点,据动量守恒求出小车和物块的末速度,再据功能关系求出小车上表面的滑动摩擦因数;(3) 物块始终不脱离轨道,即物块上升的临界最高点为C点,据动量守恒和功能关系可求出半圆弧轨道BCD的半径的临界值。
(1)对物块P的下滑过程,由机械能守恒得:![]()
解得:![]()
物块PQ发生弹性碰撞,则![]() 、
、![]()
解得:![]() ,即碰撞后瞬间物块Q的速度大小为6m/s
,即碰撞后瞬间物块Q的速度大小为6m/s
(2) 物块Q与小车相对静止时,共同速度为![]() ,系统水平方向动量守恒,则
,系统水平方向动量守恒,则
![]() ,解得:
,解得:![]()
物块Q从开始运动到与小车相对静止过程,由功能关系得:![]()
解得:![]()
(3) 物块Q滑至C点与小车共速时,半径R最小,则:
![]()
解得:![]()

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目