题目内容
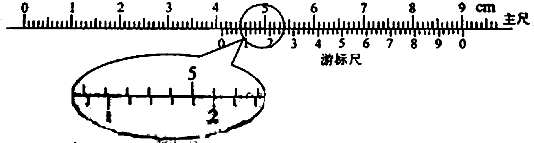
Ⅰ.某学生用打点计时器研究小车的匀变速直线运动.他将打点计时器接到频率为50Hz的交流电源上,实验时得到一条纸带.他在纸带上便于测量的地方选取第一个计时点,在这个点下标明A,第六个点下标明B,第十一个点下标明C,第十六个点下标明D,第二十一个点下标明E.测量时发现B点已模糊不清,于是他测得AC长为14.56cm、CD长为11.15cm,DE长为13.73cm,则打C点时小车的瞬时速度大小为

Ⅱ.用一测力计水平拉一端固定的弹簧,用来测量弹簧的劲度系数k,测出的拉力F与弹簧长度L之间的数据关系如下表:
(1)在图中的坐标中作出此弹簧的F-L图象; 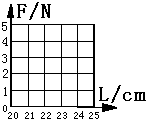
(2)图象与L轴的交点表示
(3)此弹簧的劲度系数为
0.986
0.986
m/s,小车运动的加速度大小为2.58
2.58
m/s2,AB的距离应为5.99
5.99
cm.(保留三位有效数字)
Ⅱ.用一测力计水平拉一端固定的弹簧,用来测量弹簧的劲度系数k,测出的拉力F与弹簧长度L之间的数据关系如下表:
| 拉力F/N | 1.10 | 1.50 | 2.00 | 3.00 | 3.50 | 3.80 | 4.00 |
| 弹簧长度L、cm | 22.0 | 22.35 | 22.70 | 23.31 | 23.65 | 23.80 | 24.00 |

(2)图象与L轴的交点表示
自然长度
自然长度
,其值为21.4cm
21.4cm
;(3)此弹簧的劲度系数为
约150N/m
约150N/m
.分析:根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上C点时小车的瞬时速度大小;根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小.
解答:解:(1)相邻的计数点间的时间间隔为T=0.1s,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,
得:vC=
=
=0.986m/s
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对2个加速度取平均值
得:a=
(a1+a2)
即小车运动的加速度计算表达式为:
a=
=
=2.58m/s2
根据匀变速直线运动的推论公式xm-xn=(m-n)aT2,
得:x4-x3=△x=xDE-xCD=2.58cm
由于:x1+2△x=x3=11.15cm
解得:x1=5.99cm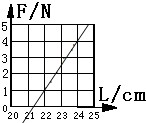
(2)①如图所示:作图时注意尽量使描出的点落在直线上,不能落在直线上的点让其分布在直线两侧.
②图象与L轴的交点表示自然长度,其值为21.4cm;
③由图象解得斜率即为劲度系数:
k=
=150N/m
故答案为:(1)0.986,2.58,5.99
(2)自然长度; 21.4cm 约150N/m.
得:vC=
| xAE |
| 4T |
| (14.56+11.15+13.73)×10-2 |
| 4×0.1 |
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2
x4-x2=2a2T2
为了更加准确的求解加速度,我们对2个加速度取平均值
得:a=
| 1 |
| 2 |
即小车运动的加速度计算表达式为:
a=
| x4+x3-x2-x1 |
| 4T2 |
| xCE-xAC |
| 4T2 |
根据匀变速直线运动的推论公式xm-xn=(m-n)aT2,
得:x4-x3=△x=xDE-xCD=2.58cm
由于:x1+2△x=x3=11.15cm
解得:x1=5.99cm

(2)①如图所示:作图时注意尽量使描出的点落在直线上,不能落在直线上的点让其分布在直线两侧.
②图象与L轴的交点表示自然长度,其值为21.4cm;
③由图象解得斜率即为劲度系数:
k=
| △F |
| △x |
故答案为:(1)0.986,2.58,5.99
(2)自然长度; 21.4cm 约150N/m.
点评:要提高应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
相关题目

 某学生用打点计时器研究小车的匀变速直线运动.他将打点计时器接到频率为50Hz的交流电源上,实验时得到一条如图所示的纸带.他在纸带上便于测量的地方选取第一个计时点,在这点下标明A,第六个计时点下标明B,第十一个计时点下标明C,第十六个计时点下标明D,测得AC长为14.56cm,BD长为19.72cm,则C点时小车的瞬时速度大小为
某学生用打点计时器研究小车的匀变速直线运动.他将打点计时器接到频率为50Hz的交流电源上,实验时得到一条如图所示的纸带.他在纸带上便于测量的地方选取第一个计时点,在这点下标明A,第六个计时点下标明B,第十一个计时点下标明C,第十六个计时点下标明D,测得AC长为14.56cm,BD长为19.72cm,则C点时小车的瞬时速度大小为