题目内容
3.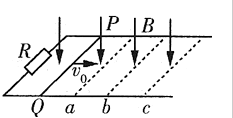 如图所示,水平光滑的平行金属导轨,左端接有电阻R,匀强磁场B竖直向下分布在导轨所在的空间内,质量一定的金属棒PQ垂直导轨放置.今使棒以一定能初速度v0向右运动,棒到位置c时速度刚好为零,设导轨与棒的电阻均不计,ab=bc,则金属棒在从a到b和从b到c的两个过程中( )
如图所示,水平光滑的平行金属导轨,左端接有电阻R,匀强磁场B竖直向下分布在导轨所在的空间内,质量一定的金属棒PQ垂直导轨放置.今使棒以一定能初速度v0向右运动,棒到位置c时速度刚好为零,设导轨与棒的电阻均不计,ab=bc,则金属棒在从a到b和从b到c的两个过程中( )| A. | 棒运动的加速度始终相等 | B. | 通过电阻R的电量之比为1:1 | ||
| C. | 通过电阻R的平均电流之比为1:1 | D. | 时间之比为($\sqrt{2}-1$):1 |
分析 金属棒向右做加速度逐渐减小的减速运动,克服安培力做功,把金属棒的动能转化为内能;由能量守恒判断回路产生的内能;由牛顿第二定律判断加速度的大小关系;由E=BLv求出感应电动势,由欧姆定律求出感应电流,最后由电流定义式的变形公式求出感应电荷量.
解答 解:A、金属棒受到的安培力F=BIL=B$\frac{BLv}{R}$L=$\frac{{B}^{2}{L}^{2}v}{R}$,金属棒受到的安培力水平向左,金属棒在安培力作用下做减速运动,速度v越来越小,安培力F逐渐减小,加速度:a=$\frac{F}{m}$=$\frac{{B}^{2}{L}^{2}v}{mR}$减小,故A错误;
B、金属棒运动过程中,电路产生的感应电荷量Q=I△t=$\frac{E}{R}$△t=$\frac{△t}{R}$×$\frac{△Φ}{△t}$=$\frac{△Φ}{R}$=B$\frac{△S}{R}$,从a到b的过程中与从b到c的过程中,回路面积的变化量△S相等,B、R相等,因此,通过棒横截面积的电荷量相等,故B正确;
C、感应电动势:E=$\frac{△Φ}{△t}$=$\frac{BS}{△t}$,金属棒做减速运动,已知:ab=bc,金属棒从a运动到b的时间比从b运动c的时间长,则从a到b的感应电动势大于从b到c的感应电动势,通过R的平均电流值不相等,通过电阻R的平均电流之比不是1:1,故C错误;
D、已知:ab=bc,如果金属棒做匀减速直线运动,金属棒在从a到b和从b到c的两个过程中的运动时间之比为($\sqrt{2}-1$):1,金属棒实际上做加速度减小的减速运动,因此运动时间之比不是($\sqrt{2}-1$):1,故D错误;
故选:B.
点评 本题考查综合运用电磁感应、电路知识、牛顿定律、等知识的能力,是一道综合题,有一定难度,分析清楚金属棒的运动过程、应用安培力公式、牛顿第二定律、运动学规律可以解题.

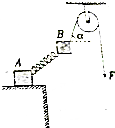 如图所示,质量分别为M、m的两个木块A、B通过劲度系数为K的轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体处于静止状态,绳与水平方向成α角,不计滑轮与绳间的摩擦,则下列说法正确的是( )
如图所示,质量分别为M、m的两个木块A、B通过劲度系数为K的轻弹簧连接,木块A放在水平桌面上,木块B用轻绳通过定滑轮在力F的作用下整体处于静止状态,绳与水平方向成α角,不计滑轮与绳间的摩擦,则下列说法正确的是( )| A. | 木块A对桌面的压力为N=Mg+mg-Fsinα | |
| B. | 轻弹簧处于拉伸状态,弹簧的弹力大小为$\sqrt{{F}^{2}-2Fmgsinα+{m}^{2}{g}^{2}}$ | |
| C. | 木块A对桌面的摩擦力大小为f=Fcosα,方向向左 | |
| D. | 木块A对桌面的摩擦力大小为f=Fsinα,方向向右 |
 如图所示为大量氮气分子在甲乙两种状态下的速率分布统计规律图,则下列说法正确的是( )
如图所示为大量氮气分子在甲乙两种状态下的速率分布统计规律图,则下列说法正确的是( )| A. | 氮气在甲状态下的温度较高 | |
| B. | 甲状态做无规则运动平均速率较大,氮气分子较多 | |
| C. | 乙状态下氮气分子做无规则运动更剧烈 | |
| D. | 某时刻速率为1000m/s的分子在下一时刻的速率一定还是1000m/s |
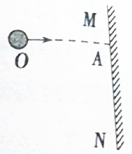 如图所示,在足够高的竖直墙壁MN的左侧某点O以不同的初速度将小球水平抛出,其中OA沿水平方向,则所有抛出的小球在碰到墙壁前瞬间,其速度的反向延长线( )
如图所示,在足够高的竖直墙壁MN的左侧某点O以不同的初速度将小球水平抛出,其中OA沿水平方向,则所有抛出的小球在碰到墙壁前瞬间,其速度的反向延长线( )| A. | 交于OA上的同一点 | |
| B. | 交于OA上的不同点,初速度越大,交点越靠近O点 | |
| C. | 交于OA上的不同点,初速度越小,交点越靠近O点 | |
| D. | 因为小球的初速度和OA距离未知,所以无法确定 |
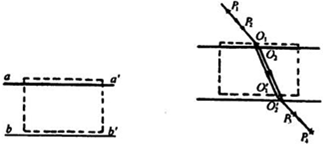
| A. | 变大 | B. | 变小 | ||
| C. | 不变 | D. | 变大、变小均有可能 |

| A. | 励磁线圈中的电流方向是逆时针方向 | |
| B. | 若只增大加速电压,可以使电子流的圆形径迹的半径增大 | |
| C. | 若只增大线圈中的电流,可以使电子流的圆形径迹的半径增大 | |
| D. | 若两线圈间的磁感应强度已知,灯丝发出的电子的初速为零,加速电压为U,则可通过测量圆形径迹的直径来估算电子的比荷 |
 某“驴友”在旅游山谷右侧时遇险,救援人员从左边山顶上,利用绳索下滑到登陆快艇,接着驾驶快艇登陆接近目标,救援被困山上的“驴友”,如图所示.若绳索两端同定好后,为保证行动安全快捷,救援队员先尢摩擦自由加速滑到某最大速度,再靠摩擦减速滑至快艇,到达快艇时速度不能超过5m/s,已知绳长224m,重力加速度g=10m/s2.
某“驴友”在旅游山谷右侧时遇险,救援人员从左边山顶上,利用绳索下滑到登陆快艇,接着驾驶快艇登陆接近目标,救援被困山上的“驴友”,如图所示.若绳索两端同定好后,为保证行动安全快捷,救援队员先尢摩擦自由加速滑到某最大速度,再靠摩擦减速滑至快艇,到达快艇时速度不能超过5m/s,已知绳长224m,重力加速度g=10m/s2.