题目内容
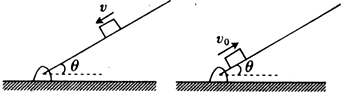
17.如图甲所示,足够长的木板与水平地面间的夹角θ=30°,可视为质点的一小木块恰好能沿着木板匀速下滑,若让该小木块从木板的底端以初速度v0=8m/s沿木板向上运动(如图乙所示),取g=10m/s2,求:(1)小木块与木板间的动摩擦因数;
(2)小木块在t=1s内沿木板滑行的距离.
分析 (1)当θ=30°时,小物块恰好能沿着木板匀速下滑,根据平衡条件和摩擦力公式列方程,可求出动摩擦因数;
(2)小物块沿木板向上滑行时,根据牛顿第二定律得出加速度,然后根据速度位移关系公式得到物块向上滑行的距离s.
解答 解:(1)小物块恰好能沿着木板匀速下滑.由平衡条件得:
mgsinθ-f=0,
f=μmgcosθ
联立解得:μ=tanθ=$\frac{\sqrt{3}}{3}$.
(2)对于小物块沿木板向上滑行,由牛顿第二定律得:
mgsinθ+μmgcosθ=ma
得a=gsin30°+μgcos30°=$10m/{s}_{\;}^{2}$
速度减为0的时间,$t=\frac{{v}_{0}^{\;}}{a}=\frac{8}{10}s=0.8s$
小物块速度减为0后,处于静止
又0-v02=-2as
代入数据得:s=$\frac{{v}_{0}^{2}}{2a}=\frac{{8}_{\;}^{2}}{2×10}=3.2m$
答:(1)小物块与木板间的动摩擦因数是$\frac{\sqrt{3}}{3}$;
(2)小物块沿木板滑行的距离s上3.2m.
点评 本题是已知受力情况确定运动情况的问题,关键是受力分析后根据牛顿第二定律列式求解加速度,然后根据运动学公式列式求解.第2小题的另一方法是:由动能定理,得:-mgsinθ•s-μmgcosθ•s=0-$\frac{1}{2}$mv02,解得s=3.2 m.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16.从地面竖直上抛一小球,设小球上升到最高点所用的时间为t1,下落到地面所用的时间为t2.若考虑到空气阻力的作用,则( )
| A. | t1=t2 | B. | t1<t2 | C. | t1>t2 | D. | 无法判断 |
17.一个物体做匀变速直线运动,它的位移与时间的关系式为x=t+0.5t2(m),从t=0时开始,运动了t1时间时,它的速度大小为5m/s,则t1为( )
| A. | 1 s | B. | 2 s | C. | 4 s | D. | 8 s |
12. 如图是我国于2016年10月19日发射的神州十一号飞船.神州十一号和天宫二号都绕地运行,神州十一号跑“内圈”追赶天宫二号,经过五次变轨,螺旋线递进,步步靠近,在距地面高393km处完成了“天神之吻”,成功对接.则( )
如图是我国于2016年10月19日发射的神州十一号飞船.神州十一号和天宫二号都绕地运行,神州十一号跑“内圈”追赶天宫二号,经过五次变轨,螺旋线递进,步步靠近,在距地面高393km处完成了“天神之吻”,成功对接.则( )
 如图是我国于2016年10月19日发射的神州十一号飞船.神州十一号和天宫二号都绕地运行,神州十一号跑“内圈”追赶天宫二号,经过五次变轨,螺旋线递进,步步靠近,在距地面高393km处完成了“天神之吻”,成功对接.则( )
如图是我国于2016年10月19日发射的神州十一号飞船.神州十一号和天宫二号都绕地运行,神州十一号跑“内圈”追赶天宫二号,经过五次变轨,螺旋线递进,步步靠近,在距地面高393km处完成了“天神之吻”,成功对接.则( )| A. | 神州十一号需要通过加速才能向“外圈”变轨 | |
| B. | 神州十一号在变轨追赶天宫二号的过程中机械能守恒 | |
| C. | 神州十一号与天宫二号对接时绕地运行的速度为零 | |
| D. | 神州十一号在“内圈”绕地运行的速度小于天宫二号绕地运行的速度 |
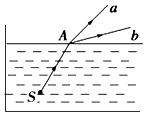
2.如图所示,水下光源S向水面A点发射一束光线,折射光线分别为a、b两束.则( )

| A. | a光的频率小于b光的频率 | |
| B. | 在真空中a光的速度大于b光的速度 | |
| C. | 若a光为绿光,则b可能为紫光 | |
| D. | 若保持入射点A位置不变,将入射光线瞬时针旋转,从水面上方观察,a光先消失 | |
| E. | 用同一双缝干涉实验装置分别用a、b光做实验,a光干涉相邻条纹间距大于b光干涉相邻条纹间距 |
9.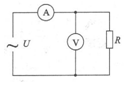 在如图所示电路中,已知交流电源电压U=311sin(100πt)V,电阻R=100欧.则电流表和电压表的读数分别为( )
在如图所示电路中,已知交流电源电压U=311sin(100πt)V,电阻R=100欧.则电流表和电压表的读数分别为( )
 在如图所示电路中,已知交流电源电压U=311sin(100πt)V,电阻R=100欧.则电流表和电压表的读数分别为( )
在如图所示电路中,已知交流电源电压U=311sin(100πt)V,电阻R=100欧.则电流表和电压表的读数分别为( )| A. | 3.11A,311V | B. | 2.2A,220V | C. | 2.2A,311V | D. | 3.11A,220V |
7.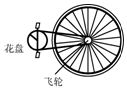 如图是自行车传动机构的示意图.假设脚跟板每2s转1圈,已知花盘半径为a,飞轮半径为r,车轮半径为R,自行车在前进过程中与路面间不打滑,则自行车前进的速率为( )
如图是自行车传动机构的示意图.假设脚跟板每2s转1圈,已知花盘半径为a,飞轮半径为r,车轮半径为R,自行车在前进过程中与路面间不打滑,则自行车前进的速率为( )
 如图是自行车传动机构的示意图.假设脚跟板每2s转1圈,已知花盘半径为a,飞轮半径为r,车轮半径为R,自行车在前进过程中与路面间不打滑,则自行车前进的速率为( )
如图是自行车传动机构的示意图.假设脚跟板每2s转1圈,已知花盘半径为a,飞轮半径为r,车轮半径为R,自行车在前进过程中与路面间不打滑,则自行车前进的速率为( )| A. | $\frac{πrR}{a}$ | B. | $\frac{πra}{R}$ | C. | $\frac{πRa}{r}$ | D. | $\frac{πR}{ar}$ |