题目内容
 (2013?山东)如图所示,一质量m=0.4kg的小物块,以v0=2m/s的初速度,在与斜面成某一夹角的拉力F作用下,沿斜面向上做匀加速运动,经t=2s的时间物块由A点运动到B点,A、B之间的距离L=10m.已知斜面倾角θ=30°,物块与斜面之间的动摩擦因数μ=
(2013?山东)如图所示,一质量m=0.4kg的小物块,以v0=2m/s的初速度,在与斜面成某一夹角的拉力F作用下,沿斜面向上做匀加速运动,经t=2s的时间物块由A点运动到B点,A、B之间的距离L=10m.已知斜面倾角θ=30°,物块与斜面之间的动摩擦因数μ=
| ||
| 3 |
(1)求物块加速度的大小及到达B点时速度的大小.
(2)拉力F与斜面的夹角多大时,拉力F最小?拉力F的最小值是多少?
分析:(1)物体做匀加速直线运动,根据运动学公式求解加速度和末速度;
(2)对物体受力分析,受重力、拉力、支持力和滑动摩擦力,根据牛顿第二定律列式求解出拉力F的表达式,分析出最小值.
(2)对物体受力分析,受重力、拉力、支持力和滑动摩擦力,根据牛顿第二定律列式求解出拉力F的表达式,分析出最小值.
解答:解:(1)物体做匀加速直线运动,根据运动学公式,有:
L=v0t+
at2 ①
v=v0+at ②
联立解得;
a=3m/s2
v=8m/s
(2)对物体受力分析,受重力、拉力、支持力和滑动摩擦力,如图
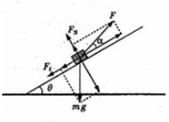
根据牛顿第二定律,有:
平行斜面方向:Fcosα-mgsin30°-Ff=ma
垂直斜面方向:Fsinα+FN-mgcoscos30°=0
其中:Ff=μFN
联立解得:
F=
=
故当α=30°时,拉力F有最小值,为Fmin=
N;
答:(1)物块加速度的大小为3m/s2,到达B点的速度为8m/s;
(2)拉力F与斜面的夹角30°时,拉力F最小,最小值是
N.
L=v0t+
| 1 |
| 2 |
v=v0+at ②
联立解得;
a=3m/s2
v=8m/s
(2)对物体受力分析,受重力、拉力、支持力和滑动摩擦力,如图

根据牛顿第二定律,有:
平行斜面方向:Fcosα-mgsin30°-Ff=ma
垂直斜面方向:Fsinα+FN-mgcoscos30°=0
其中:Ff=μFN
联立解得:
F=
| mg(sinα+μcosα)+ma |
| cosα+μsinα |
| mg(sinα+μcosα)+ma | ||||
|
故当α=30°时,拉力F有最小值,为Fmin=
13
| ||
| 5 |
答:(1)物块加速度的大小为3m/s2,到达B点的速度为8m/s;
(2)拉力F与斜面的夹角30°时,拉力F最小,最小值是
13
| ||
| 5 |
点评:本题是2013年山东卷高考理综试题第22题,是已知运动情况确定受力情况,关键先根据运动学公式求解加速度,然后根据牛顿第二定律列式讨论.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 (2013?山东)如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、
(2013?山东)如图所示,在x轴上相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、 (2013?山东)图甲是小型交流发电机的示意图,两磁极N、S间的磁场可视为水平方向的匀强磁场,A为交流电流表.线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动.从图示位置开始计时,产生的交变电流随时间变化的图象如图乙所示.以下判断正确的是( )
(2013?山东)图甲是小型交流发电机的示意图,两磁极N、S间的磁场可视为水平方向的匀强磁场,A为交流电流表.线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动.从图示位置开始计时,产生的交变电流随时间变化的图象如图乙所示.以下判断正确的是( )
