题目内容
15. 如图所示,在倾角θ=37°的足够长斜面上,有一质量m=2.0kg的物块由静止开始沿斜面下滑.当物块下滑x=2m时,其速度为v=4m/s.求:
如图所示,在倾角θ=37°的足够长斜面上,有一质量m=2.0kg的物块由静止开始沿斜面下滑.当物块下滑x=2m时,其速度为v=4m/s.求:(1)物块受到的阻力?
(2)物块与斜面间的动摩擦系数?(sin37°=0.6,cos37°=0.8,g取10m/s2)
分析 (1)根据物体的运动求得加速度,由牛顿运动定律和运动学公式求得木块受到的阻力;
(2)根据受力分析求得物块与斜面间的弹力,再根据摩擦定律求得动摩擦因数.
解答 解:(1)由题意知,物块下滑时的加速度
a=$\frac{{v}^{2}-{v}_{0}^{2}}{2x}=\frac{{4}^{2}-0}{2×2}m/{s}^{2}=4m/{s}^{2}$对物块进行受力分析,根据牛顿第二定律有:
mgsin37°-f=ma
可得物体受到的摩擦力f=mgsin37°-ma=2×10×0.6-2×4N=4N
(2)在垂直斜面方向物体所受合力为零有:
N-mgcos37°=0
滑动摩擦力f=μN
由此可得物块与斜面间的动摩擦因数μ=$\frac{f}{N}=\frac{4}{2×10×0.8}=0.25$
答:(1)物块受到的阻力为4N;
(2)物块与斜面间的动摩擦因数为0.25.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁,基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.氢原子的部分能级如图所示.已知可见光的光子能量在1.62eV到3.11eV之间.由此可推知,氢原子( )


| A. | 从高能级向n=1能级跃迁时发出的光的波长比可见光的短 | |
| B. | 从高能级向n=2能级跃迁时发出的光均为可见光 | |
| C. | 从高能级向n=3能级跃迁时发出的光的频率比可见光的高 | |
| D. | 从n=2能级向n=1能级跃迁时发出的光为可见光 |
6. 如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
 如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )
如图,A、B、C三点为一直角三角形的三个顶点,∠B=30°,现在A、B两点放置两点电荷qA、qB,测得C点场强方向与BA平行,则关于qA、qB的电性及其大小关系,下列说法中正确的是( )| A. | qA一定带正电 | B. | qB一定带正电 | C. | qA:qB=1:4 | D. | qA:qB=1:8 |
10. 如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )
如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )
 如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )
如图所示,线段A为某电源的U-I图线,线段B为某电阻的U-I图线,将上述电源和电阻组成闭合电路时,下列说法正确的是( )| A. | 电阻B的阻值为1Ω | B. | 电源的总功率为5W | ||
| C. | 电源的输出功率为4W | D. | 电源的效率为50% |
7.简谐横波某时刻的波形图线如图所示,a为介质中的一个质点,由图象可知( )


| A. | 此时质点a的加速度方向一定沿y轴负方向 | |
| B. | 此时质点a的速度方向一定沿y轴负方向 | |
| C. | 若波向左传播,则此时a的速度方向一定沿y轴负方向 | |
| D. | 若波向右传播,则此时a的速度方向一定沿y轴负方向 |
4.在图中,叠放在物体C的斜面上的物体A与B,共同沿斜面匀速下滑,下列说法正确的是( )
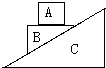

| A. | A物体受重力和B对A的支持力 | |
| B. | B物体受重力、A给的压力、C给的支持力 | |
| C. | B物体受重力、A对B的压力和静摩擦力、C对B的支持力和滑动摩擦力 | |
| D. | C物体的斜面受到B对C的压力,B对C的摩擦力 |