题目内容
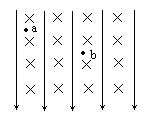
如下图所示,某空间存在垂直纸面向外的匀强磁场,磁感应强度为B,虚线MN为一竖直界面,界面左侧还有水平向右的匀强电场。长为l绝缘细杆水平固定在离地面高度也为l处,B端在界面上。有一带正电的小环穿在细杆上从A端由静止释放,小环先加速后匀速穿过B端,进入磁场中做匀速圆周运动,在沿圆周运动的过程中,某时刻磁场突然消失,结果小环以与水平成60°角的方向落在B点正下方的地面上的C点,已知小环的质量为m、电量为q、与细杆的动摩擦因数为μ,小环重力不计,试求:
(1)小环进入界面右侧时的速度。
(2)小环脱离细杆到落地所用时间。
(3)小环从A到B克服摩擦力所做的功。
解:(1)如图所示,设小环运动到D点磁场消失,在△OCD中,∠OCD=30°,
所以R=OC×sin30°①

OC=2R②
BC=R+OC③
所以R=![]() ④
④
由qvB=m![]() ⑤
⑤
得R=![]() =
=![]()
所以v=![]() ⑥
⑥
(2)设在磁场中运动的时间为t1,磁场消失后小环做匀速直线运动时间为t2,则
t1=![]() ⑦
⑦
CD=![]() R=
R=![]() ⑧
⑧
t2=![]() ⑨
⑨
所以t=t1+t2=(![]() )
)![]() ⑩
⑩
(3)小环在AB杆上匀速运动时,根据平衡条件有:f洛=FN![]()
Ff=Eq![]()
又有Ff=μFN![]()
解得E=μBv=![]()
![]()
从A运动到B应用动能定理,有
W电-Wf=![]() mv2
mv2![]()
Wf=W电-![]() mv2
mv2
=Eql-![]() mv2
mv2
=![]() (6μ-1)
(6μ-1)![]()

练习册系列答案
相关题目
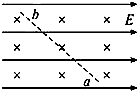 如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直纸面向里,一带电微粒由a点进入电磁场并刚好能沿ab直线向上运动.下列说法正确的是( )
如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直纸面向里,一带电微粒由a点进入电磁场并刚好能沿ab直线向上运动.下列说法正确的是( )| A、微粒一定带负电 | B、微粒动能一定减小 | C、微粒的电势能一定增加 | D、微粒的机械能不变 |
 如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直纸面向里,一带电微粒由A点进入电磁场并刚好能沿AB直线向上运动,则该微位在A、B两点的动能Ek和电势能EP的关系是( )
如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直纸面向里,一带电微粒由A点进入电磁场并刚好能沿AB直线向上运动,则该微位在A、B两点的动能Ek和电势能EP的关系是( )