题目内容
 (2009?诸城市模拟)如图,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10米,BC长1米,AB和CD轨道光滑.一质量为1千克的物体,从A点以4米/秒的速度开始运动,经过BC后滑到高出C点10.3m的D点速度为零.求:(g=10m/s2)
(2009?诸城市模拟)如图,ABCD为一竖直平面的轨道,其中BC水平,A点比BC高出10米,BC长1米,AB和CD轨道光滑.一质量为1千克的物体,从A点以4米/秒的速度开始运动,经过BC后滑到高出C点10.3m的D点速度为零.求:(g=10m/s2)(1)物体与BC轨道的滑动摩擦系数.
(2)物体第5次经过B点时的速度.(结果用根式表示)
(3)物体最后停止的位置(距B点).
分析:(1)分析从A到D过程,由动能定理求解.
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理求解.
(3)分析整个过程,由动能定理求解.
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理求解.
(3)分析整个过程,由动能定理求解.
解答:解:(1)分析从A到D过程,由动能定理得
-mg(h-H)-μmgSBC=0-
m
解得μ=0.5
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
mgH-μmg4SBC=
-
解得v2=4
m/s
(3)分析整个过程,由动能定理得
mgH-μmgs=0-
解得s=21.6m
所以物体在轨道上来回了10次后,还有1.6m,故离B的距离为2m-1.6m=0.4m
答:(1)物体与BC轨道的滑动摩擦系数是0.5.
(2)物体第5次经过B点时的速度是4
m/s
(3)物体最后停止的位置离B的距离为0.4m
-mg(h-H)-μmgSBC=0-
| 1 |
| 2 |
| v | 2 1 |
解得μ=0.5
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
mgH-μmg4SBC=
| 1 |
| 2 |
| mv | 2 2 |
| 1 |
| 2 |
| mv | 2 1 |
解得v2=4
| 11 |
(3)分析整个过程,由动能定理得
mgH-μmgs=0-
| 1 |
| 2 |
| mv | 2 1 |
解得s=21.6m
所以物体在轨道上来回了10次后,还有1.6m,故离B的距离为2m-1.6m=0.4m
答:(1)物体与BC轨道的滑动摩擦系数是0.5.
(2)物体第5次经过B点时的速度是4
| 11 |
(3)物体最后停止的位置离B的距离为0.4m
点评:选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.
动能定理的应用范围很广,可以求速度、力、功、位移等物理量.
动能定理的应用范围很广,可以求速度、力、功、位移等物理量.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 (2009?诸城市模拟)某带电粒子仅在电场力作用下由A点运动到B点,电力线、粒子在A点的初速度以及运动轨迹如图所示.由此可以判定( )
(2009?诸城市模拟)某带电粒子仅在电场力作用下由A点运动到B点,电力线、粒子在A点的初速度以及运动轨迹如图所示.由此可以判定( )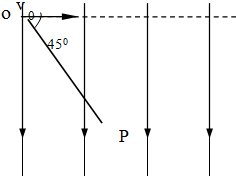 (2009?诸城市模拟)如图所示,地面上某区域存在着竖直向下的匀强电场,一个质量为m的带负电的小球以水平方向的初速度v0由O点射入该区域,刚好通过竖直平面中的P点,已知连线OP与初速度方向的夹角为45°,则此带电小球通过P点时的动能为( )
(2009?诸城市模拟)如图所示,地面上某区域存在着竖直向下的匀强电场,一个质量为m的带负电的小球以水平方向的初速度v0由O点射入该区域,刚好通过竖直平面中的P点,已知连线OP与初速度方向的夹角为45°,则此带电小球通过P点时的动能为( ) (2009?诸城市模拟)2008年9月我国成功发射了“神州七号”载人飞船.为了观察“神舟七号”的运行和宇航员仓外活动情况,飞船利用弹射装置发射一颗“伴星”.伴星经调整后,和“神舟七号”一样绕地球做匀速圆周运动,但比“神舟七号”离地面稍高一些,如图所示,那么( )
(2009?诸城市模拟)2008年9月我国成功发射了“神州七号”载人飞船.为了观察“神舟七号”的运行和宇航员仓外活动情况,飞船利用弹射装置发射一颗“伴星”.伴星经调整后,和“神舟七号”一样绕地球做匀速圆周运动,但比“神舟七号”离地面稍高一些,如图所示,那么( )