题目内容
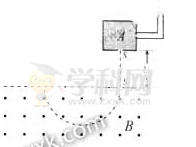
对铀235的进一步研究在核能的开发和利用中具有重要意义．如图所示，质量为m、电荷量为q的铀235离子，从容器A下方的小孔S1不断飘入加速电场，其初速度可视为零，然后经过小孔S2垂直于磁场方向进入磁感应强度为B的匀强磁场中，做半径为R的匀速圆周运动．离子行进半个圆周后离开磁场并被收集，离开磁场时离子束的等效电流为I．不考虑离子重力及离子间的相互作用．（1）求加速电场的电压U；
（2）求出在离子被收集的过程中任意时间t内收集到离子的质量M；
（3）实际上加速电压的大小会在U±△U范围内微小变化．若容器A中有电荷量相同的铀235和铀238两种离子，如前述情况它们经电场加速后进入磁场中会发生分离，为使这两种离子在磁场中运动的轨迹不发生交叠，
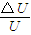应小于多少？（结果用百分数表示，保留两位有效数字）
【答案】分析：（1）设离子经电场加速度时的速度为v，由动能定理及向心力公式即可求解；
（2）设在t时间内收集到的离子个数为N，总电荷量为Q，根据Q=It、M=Nm，即可求解M；
（3）根据向心力公式求出半径R的表达式，进而表示出铀235离子在磁场中最大半径和铀238离子在磁场中最小半径，要使两种离子在磁场中运动的轨迹不发生交叠，则铀235离子在磁场中最大半径小于铀238离子在磁场中最小半径，进而即可求解．
解答：解：（1）设离子经电场加速度时的速度为v，由动能定理得：
qU=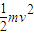
…①
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，即：Bqv=m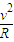
…②
由①②解得：U=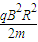
…③
（2）设在t时间内收集到的离子个数为N，总电荷量为Q，则Q=It…④
N=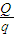
…⑤
M=Nm…⑥
由④⑤⑥式解得：M=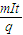
（3）由①②式得：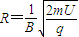
设m′为铀238离子的质量，由于电压在U±△U范围内微小变化，铀235离子在磁场中最大半径为：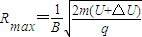
铀238离子在磁场中最小半径为：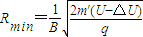
这两种离子在磁场中运动的轨迹不发生交叠的条件为：Rmax＜Rmin
即：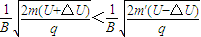
则有：m（U+△U）＜m′（U-△U）
所以：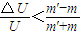
其中铀235离子质量m=235u（u为原子质量单位），其中铀238离子质量m′=238u
故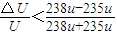
解得：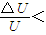
0.63%
答：（1）加速电场的电压为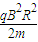
；
（2）在离子被收集的过程中任意时间t内收集到离子的质量为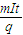
；
（3）为使这两种离子在磁场中运动的轨迹不发生交叠，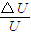
应小于0.63%．
点评：本题主要考查了动能定理及向心力公式的直接应用，要求同学们知道要使两种离子在磁场中运动的轨迹不发生交叠，则铀235离子在磁场中最大半径小于铀238离子在磁场中最小半径，难度适中．
（2）设在t时间内收集到的离子个数为N，总电荷量为Q，根据Q=It、M=Nm，即可求解M；
（3）根据向心力公式求出半径R的表达式，进而表示出铀235离子在磁场中最大半径和铀238离子在磁场中最小半径，要使两种离子在磁场中运动的轨迹不发生交叠，则铀235离子在磁场中最大半径小于铀238离子在磁场中最小半径，进而即可求解．
解答：解：（1）设离子经电场加速度时的速度为v，由动能定理得：
qU=
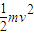…①粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，即：Bqv=m
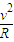…②由①②解得：U=
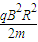…③（2）设在t时间内收集到的离子个数为N，总电荷量为Q，则Q=It…④
N=
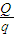…⑤M=Nm…⑥
由④⑤⑥式解得：M=
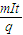
（3）由①②式得：
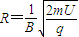
设m′为铀238离子的质量，由于电压在U±△U范围内微小变化，铀235离子在磁场中最大半径为：
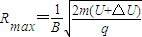
铀238离子在磁场中最小半径为：
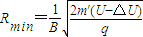
这两种离子在磁场中运动的轨迹不发生交叠的条件为：Rmax＜Rmin
即：
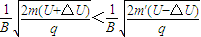
则有：m（U+△U）＜m′（U-△U）
所以：
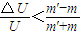
其中铀235离子质量m=235u（u为原子质量单位），其中铀238离子质量m′=238u
故
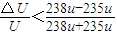
解得：
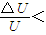0.63%答：（1）加速电场的电压为
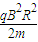；（2）在离子被收集的过程中任意时间t内收集到离子的质量为
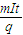；（3）为使这两种离子在磁场中运动的轨迹不发生交叠，
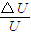应小于0.63%．点评：本题主要考查了动能定理及向心力公式的直接应用，要求同学们知道要使两种离子在磁场中运动的轨迹不发生交叠，则铀235离子在磁场中最大半径小于铀238离子在磁场中最小半径，难度适中．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
对铀235的进一步研究在核能的开发和利用中具有重要意义．如图所示，质量为m、电荷量为q的铀235离子，从容器A下方的小孔S1不断飘入加速电场，其初速度可视为零，然后经过小孔S2垂直于磁场方向进入磁感应强度为B的匀强磁场中，做半径为R的匀速圆周运动．离子行进半个圆周后离开磁场并被收集，离开磁场时离子束的等效电流为I．不考虑离子重力及离子间的相互作用．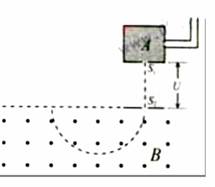
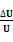应小于多少？（结果用百分数表示，保留两位有效数字）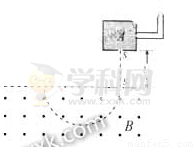
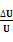应小于多少？（结果用百分数表示，保留两位有效数字）