题目内容
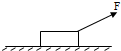
质量为10kg的箱子放在水平地面上，箱子和地面的滑动摩擦因数为0.5，现用倾角为37°的100N力拉箱子，箱子从静止开始运动，如图所示，2S末撤去拉力．
求：（Sin37°=0.6，Cos37°=0.8，g=10m/s2）
（1）撤去拉力时箱子的速度为多少？
（2）箱子继续运动多长时间才能静止？
解：（1）物体在拉力F作用下加速滑行，受重力、拉力、支持力和滑动摩擦力，根据牛顿第二定律，有：
Fcosθ-μ（mg-Fsinθ）=ma1，
解得a1=6m/s2，
根据速度时间关系公式，2s末速度为：v=a1t1=6×2=12m/s；
（2）撤去拉力后，物体由于惯性继续滑行，受重力、支持力和滑动摩擦力，根据牛顿第二定律，有：
μmg=ma2，
解得a2=5m/s2，
匀减速过程，根据速度时间关系公式，有v=a2t2
解得t2=2.4s；
（1）撤去拉力时箱子的速度为12m/s；
（2）箱子继续运动2.4s时间才能静止．
分析：（1）由牛顿第二定律可求得前2s的加速度，则可求得2s末的速度；
（2）撤去拉力后，物体在摩擦力的作用下匀减速运动，由速度公式可求得减速的时间．
点评：本题关键是明确箱子的运动规律，要注意加速和减速过程的正压力不同导致滑动摩擦力不同，不难．
Fcosθ-μ（mg-Fsinθ）=ma1，
解得a1=6m/s2，
根据速度时间关系公式，2s末速度为：v=a1t1=6×2=12m/s；
（2）撤去拉力后，物体由于惯性继续滑行，受重力、支持力和滑动摩擦力，根据牛顿第二定律，有：
μmg=ma2，
解得a2=5m/s2，
匀减速过程，根据速度时间关系公式，有v=a2t2
解得t2=2.4s；
（1）撤去拉力时箱子的速度为12m/s；
（2）箱子继续运动2.4s时间才能静止．
分析：（1）由牛顿第二定律可求得前2s的加速度，则可求得2s末的速度；
（2）撤去拉力后，物体在摩擦力的作用下匀减速运动，由速度公式可求得减速的时间．
点评：本题关键是明确箱子的运动规律，要注意加速和减速过程的正压力不同导致滑动摩擦力不同，不难．
练习册系列答案
相关题目
在学校组织的“运箱子比赛”趣味体育活动中，一名学生用大小为F=100N的力先后两次作用在水平面上的质量为m=10kg的箱子上，如图所示．一次箱子做匀速运动，一次做匀加速运动．已知sin37°=0.6，cos37°=0.8，重力加速度取g=10m/s2．求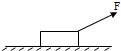
质量为10kg的箱子放在水平地面上，箱子和地面的滑动摩擦因数为0.5，现用倾角为37°的100N力拉箱子，箱子从静止开始运动，如图所示，2S末撤去拉力．
