题目内容
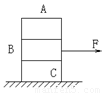
 如图A、B、C三个物块叠放在光滑水平面上,三物块质量均为m,AB间动摩擦因数为3μ,BC间动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.由静止开始,对中间的物块B施加水平拉力F,当F较小时三物块相对静止共同加速,当F较大时可将B从AC间抽出来.下面四个值中选出能将B抽出的F的最小值为( )
如图A、B、C三个物块叠放在光滑水平面上,三物块质量均为m,AB间动摩擦因数为3μ,BC间动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力.由静止开始,对中间的物块B施加水平拉力F,当F较小时三物块相对静止共同加速,当F较大时可将B从AC间抽出来.下面四个值中选出能将B抽出的F的最小值为( )| A、5μmg | B、7μmg | C、8.5μmg | D、10μmg |
分析:先求出相对静止时各物体允许的增大加速度,在根据牛顿第二定律求解.
解答:解:在摩擦力的作用下,A物体的最大加速度aA=
=3μg;在摩擦有的作用下,C物体的最大加速度aC=
=2μg 要想将B从中间抽出,应使加速度aB>3μg
此时,aB=
>3μg
可得F>8μmg,因此C正确.
故选:C.
| 3μmg |
| m |
| 2mgμ |
| m |
此时,aB=
| F-2μmg-3μmg |
| m |
可得F>8μmg,因此C正确.
故选:C.
点评:本题关键灵活地选择研究对象,运用牛顿第二定律列式求解出各个临界状态的情况,较难.

练习册系列答案
相关题目
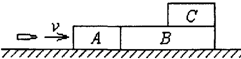 如图所示,A、B、C三个物块,质量关系是mB=2mA=2mC,A、B放在光滑水平面上,C、B、A间接触面也是光滑的,一颗子弹水平从A射入,最后从B穿出.则子弹穿出B后,三物块的速率关系正确的是( )
如图所示,A、B、C三个物块,质量关系是mB=2mA=2mC,A、B放在光滑水平面上,C、B、A间接触面也是光滑的,一颗子弹水平从A射入,最后从B穿出.则子弹穿出B后,三物块的速率关系正确的是( )| A、vA=vB=vC | B、vA>vB>vC | C、vB>vA>vC | D、vA<vB=vC |
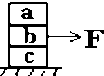 如图:a、b、c三个物块之间和与桌面接触处均有摩擦,但摩擦因数不同.当b受一水平力F作用时,a、c随b一起保持相对静止向右作匀速运动,此时( )
如图:a、b、c三个物块之间和与桌面接触处均有摩擦,但摩擦因数不同.当b受一水平力F作用时,a、c随b一起保持相对静止向右作匀速运动,此时( ) 如图所示A、B、C三个物块叠放在一起,A与B、B与C之间的动摩擦因数相同,水平面光滑,B与竖直墙之间夹着一根被压缩了的弹簧,原来A、B、C被控制,处于静止状态,在突然撤去控制后瞬间,A、B、C的运动情况可能是( )
如图所示A、B、C三个物块叠放在一起,A与B、B与C之间的动摩擦因数相同,水平面光滑,B与竖直墙之间夹着一根被压缩了的弹簧,原来A、B、C被控制,处于静止状态,在突然撤去控制后瞬间,A、B、C的运动情况可能是( )