题目内容
9. 如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平方向射中木块,并最终留在木块中与木块一起以速度v运动,若木块对子弹的阻力大小为f,视为恒定,求:从子弹进入木块开始到两者相对静止时,木块前进距离L及子弹进入木块的深度s的大小.
如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平方向射中木块,并最终留在木块中与木块一起以速度v运动,若木块对子弹的阻力大小为f,视为恒定,求:从子弹进入木块开始到两者相对静止时,木块前进距离L及子弹进入木块的深度s的大小.
分析 子弹射入木块过程,子弹和木块构成的系统动量守恒,根据动量守恒定律列式求解共同速度;然后对子弹和木块分别利用动能定理列式求解即可.
解答 解:子弹射入木块过程,系统动量守恒,故:
mv0=(M+m)v ①
对子弹,根据动能定理,有:
-f(s+L)=$\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}_{0}^{2}$ ②
对木块,根据动能定理,有:
fL=$\frac{1}{2}M{v}^{2}-0$ ③
联立解得:
L=$\frac{Mm{v}_{0}^{2}}{2(M+m)^{2}f}$
s=$\frac{{(M}^{2}+Mm+{m}^{2}){v}_{0}^{2}}{2(M+m)}$
答:从子弹进入木块开始到两者相对静止时,木块前进距离L为$\frac{Mm{v}_{0}^{2}}{2{(M+m)}^{2}f}$,子弹进入木块的深度s的大小为$\frac{{(M}^{2}+Mm+{m}^{2}){v}_{0}^{2}}{2(M+m)}$.
点评 本题关键是明确子弹和木块系统的动量守恒,然后结合动能定理对子弹和木块分别列式求解,基础题目.

练习册系列答案
相关题目
4. 如图所示,一带电荷量+Q的细木棍.在过中点c垂直于细木棍的直线上有a,b,d三点,a和b,b和c,c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则细木棍上所带电荷Q在d点处场强的大小为(k为静电力常量)( )
如图所示,一带电荷量+Q的细木棍.在过中点c垂直于细木棍的直线上有a,b,d三点,a和b,b和c,c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则细木棍上所带电荷Q在d点处场强的大小为(k为静电力常量)( )
 如图所示,一带电荷量+Q的细木棍.在过中点c垂直于细木棍的直线上有a,b,d三点,a和b,b和c,c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则细木棍上所带电荷Q在d点处场强的大小为(k为静电力常量)( )
如图所示,一带电荷量+Q的细木棍.在过中点c垂直于细木棍的直线上有a,b,d三点,a和b,b和c,c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则细木棍上所带电荷Q在d点处场强的大小为(k为静电力常量)( )| A. | k$\frac{q}{{R}^{2}}$ | B. | k$\frac{Q}{{R}^{2}}$ | C. | k$\frac{q+Q}{{R}^{2}}$ | D. | k$\frac{10q}{9{R}^{2}}$ |
14. 如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验,若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ.重力加速度为g.要使纸板相对砝码运动,所需拉力的大小至少应大于( )
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验,若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ.重力加速度为g.要使纸板相对砝码运动,所需拉力的大小至少应大于( )
 如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验,若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ.重力加速度为g.要使纸板相对砝码运动,所需拉力的大小至少应大于( )
如图所示,将小砝码置于桌面上的薄纸板上,用水平向右的拉力将纸板迅速抽出,砝码的移动很小,几乎观察不到,这就是大家熟悉的惯性演示实验,若砝码和纸板的质量分别为2m和m,各接触面间的动摩擦因数均为μ.重力加速度为g.要使纸板相对砝码运动,所需拉力的大小至少应大于( )| A. | 3μmg | B. | 4μmg | C. | 5μmg | D. | 6μmg |
5. 如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力同时推A和B,它们均静止不动.则( )
如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力同时推A和B,它们均静止不动.则( )
 如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力同时推A和B,它们均静止不动.则( )
如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力同时推A和B,它们均静止不动.则( )| A. | A与B之间一定存在摩擦力 | |
| B. | B与地之间可能存在摩擦力 | |
| C. | B对A的支持力一定小于mg | |
| D. | 地面对B的支持力的大小一定等于(M+m)g |
3.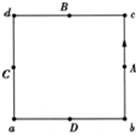 一质点沿一边长为2m的正方形轨道运动,每秒钟匀速移动1m,初始位置在bc边的中点A,由b向c运动,如图所示,A、B、C、D分别是bc、cd、da、ab边的中点,则下列说法正确的是( )
一质点沿一边长为2m的正方形轨道运动,每秒钟匀速移动1m,初始位置在bc边的中点A,由b向c运动,如图所示,A、B、C、D分别是bc、cd、da、ab边的中点,则下列说法正确的是( )
 一质点沿一边长为2m的正方形轨道运动,每秒钟匀速移动1m,初始位置在bc边的中点A,由b向c运动,如图所示,A、B、C、D分别是bc、cd、da、ab边的中点,则下列说法正确的是( )
一质点沿一边长为2m的正方形轨道运动,每秒钟匀速移动1m,初始位置在bc边的中点A,由b向c运动,如图所示,A、B、C、D分别是bc、cd、da、ab边的中点,则下列说法正确的是( )| A. | 第2s末的瞬时速度是1m/s | B. | 前2s内的平均速度为$\frac{\sqrt{2}}{2}$m/s | ||
| C. | 前4s内的平均速率为0.5m/s | D. | 前2s内的平均速度为2m/s |
 一个质量m=0.1g的小滑块,带有q=5×10-4C的电荷量放置在倾角α=60°的光滑斜面上(绝缘).斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向外,如图所示,小滑块由静止开始沿斜面滑下,其斜面足够长,小滑块至某一位置时,要离开斜面.求:
一个质量m=0.1g的小滑块,带有q=5×10-4C的电荷量放置在倾角α=60°的光滑斜面上(绝缘).斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向外,如图所示,小滑块由静止开始沿斜面滑下,其斜面足够长,小滑块至某一位置时,要离开斜面.求: 在把电流表改装为电压表的实验中,提供的器材有
在把电流表改装为电压表的实验中,提供的器材有 如图所示,粗细均为的U形管水平部分长为L,管中盛有一定质量的液体,当U形管以加速度a向右运动时,两管内液面的高度差△h=$\frac{La}{g}$.
如图所示,粗细均为的U形管水平部分长为L,管中盛有一定质量的液体,当U形管以加速度a向右运动时,两管内液面的高度差△h=$\frac{La}{g}$. 如图,一个传送带倾斜放置,倾角α=53°,传送带的动摩擦因数为μ=0.5,长度L=10m,传送带沿顺时针方向转动,一个质量m=1kg的物体1在光滑的平台上向右做匀速直线运动,速度大小为V0,在平台末端,物体1和静止的相同质量的物体2发生弹性碰撞,碰撞后物体2水平抛出,当物体2运动到传送带上表面顶端A点时,速度方向刚好和传送带上表面平行,即物体2无碰撞地运动到传送带上,已知斜面顶端与平台的高度差h=0.8m,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求:
如图,一个传送带倾斜放置,倾角α=53°,传送带的动摩擦因数为μ=0.5,长度L=10m,传送带沿顺时针方向转动,一个质量m=1kg的物体1在光滑的平台上向右做匀速直线运动,速度大小为V0,在平台末端,物体1和静止的相同质量的物体2发生弹性碰撞,碰撞后物体2水平抛出,当物体2运动到传送带上表面顶端A点时,速度方向刚好和传送带上表面平行,即物体2无碰撞地运动到传送带上,已知斜面顶端与平台的高度差h=0.8m,重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6.求: