题目内容

一修路工在S=100m的隧道中，突然发现一列火车出现在离右道口200m处，修路工恰在无论向右还是向左跑均能安全脱离危险的位置．问这位置离左出口的距离多少？他奔跑的速度至少是火车速度的多少倍？

解：要脱离危险必须使人在火车到达隧道口前跑出隧道．设人所在位置离左出口为xm，知图所示，则离右出口为（100-x）m．
v_人为人的速度，v_车为车的速度．
从左出口人恰能脱离危险时有： $\text{[math]}$
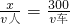
从右出口人恰能脱离危险时有： $\text{[math]}$
由上式可得：x=60m，即人离左出口60m， $\text{[math]}$ = $\text{[math]}$
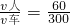即人的最小速度是火车速度的 $\text{[math]}$ 倍
答：该位置离出口60m；人的速度为火车速度的 $\text{[math]}$ 倍．
分析：画出运动情景图象，根据追及相遇问题的条件分析人与车间的位移关系，则由公式可解得人所处的距离，及人跑的速度．
点评：对于追及问题要注意画出运动过程图，再由运动公式列式求解即可，要注意中间量的引入，列方程求解．