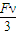Question

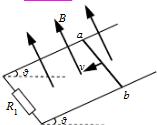
如图所示，两条电阻不计的平行导轨与水平面成 θ 角，导轨的一端连接定值电阻 R₁，匀强磁场垂直穿过导轨平面．一根质量为 m、电阻为 R₂ 的导体棒 ab，垂直导轨放置，导体棒与导轨之间的动摩擦因数为 μ，且 R₂=2R₁．如果导轨以速度 v 匀速下滑，导轨此时受到的安培力大小为 F，则以下判断正确的是（　　）

• A、电阻R₁消耗的热功率为

  Fν

  3

• B、整个装置消耗的机械功率为Fν
• C、整个装置因摩擦而消耗的热功率为μmgν?cosθ
• D、若使导体棒以 v 的速度匀速上滑，则必须施加沿导轨向上外力F_外=2F

Answer 1

分析：由题，导体棒以速度 v 匀速下滑，受到的安培力大小为 F，根据E=BLv、I=

E

R1+R2

、F=BIL，推导出BL．电阻R₁消耗的热功率为P=I²R₁，联立解得P；
根据能量转化情况，分析整个装置消耗的机械功率和因摩擦而消耗的热功率；若使导体棒以 v 的速度匀速上滑，根据平衡条件求得外力F_外．

解答：解：A、导体棒以速度v匀速下滑时，由E=BLv、I=

E

R1+R2

、F=BIL得  安培力F=

B2L2v

R1+R2

…①
电阻R₁消耗的热功率为P=I²R₁=（

BLv

R1+R2

）² R₁…②
又R₂=2R₁ …③
联立①②③解得，P=

Fv

3

  故A正确．
B、根据平衡条件可知：对导体棒：mgsinθ=F+f…④
则mgsinθ＞F，整个装置消耗的机械功率为mgsinv＞Fv．故B错误．
C、整个装置因摩擦而消耗的热功率为P_f=fv=μmgν?cosθ．故C正确．
D、若使导体棒以 v 的速度匀速上滑，安培力大小不变，方向沿斜面向下，根据平衡条件得：F_外=mgsinθ+f+F ⑤
由④⑤得 F_外=2（f+F）．故D错误．
故选AC

点评：本题综合考查了共点力平衡以及能量守恒．关键理清导体棒的运动情况，选择合适的定律进行求解．