题目内容
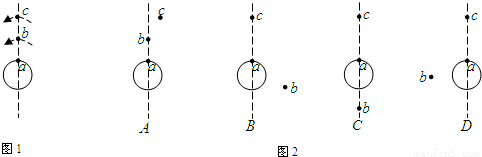
(1)设a是地球赤道上一栋建筑,b是在赤道平面内做匀速圆周运动、距地面9.6×106m的卫星,c是地球同步卫星,则b卫星的运动周期T=
(取地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,π=
) 
(2)有A、B两球在光滑水平面上沿着一条直线运动,它们发生碰撞后粘在一起,已知碰前两球的动量分别为PA=20kgm/s和PB=15kgm/s,碰撞后B球的动量改变了△PB=-5kgm/s,则碰撞后A球的动量为PA/=
5.56
5.56
h;如果某一时刻b、c刚好位于a的正上方(如图1所示),经48h,a、b、c的大致位置是图2中的B
B
.(取地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,π=
| 10 |

(2)有A、B两球在光滑水平面上沿着一条直线运动,它们发生碰撞后粘在一起,已知碰前两球的动量分别为PA=20kgm/s和PB=15kgm/s,碰撞后B球的动量改变了△PB=-5kgm/s,则碰撞后A球的动量为PA/=
25
25
kgm/s,碰撞前两球的速度大小之比vA:vB=8:15
8:15
.分析:(1)该题主要考查同步卫星,近地卫星及赤道上的物体间的追赶问题.对于不同轨道上的追赶问题,我们要从不同卫星的角速度或周期关系出发去解决问题.
(2)AB球碰撞过程中动量守恒,根据动量守恒定律即可求解.
(2)AB球碰撞过程中动量守恒,根据动量守恒定律即可求解.
解答:解:(1)由于a物体和同步卫星c的周期都为24h.所以48h后两物体又回到原位置,
根据万有引力提供向心力得:G
=m
解得:T=
G
=mg
而b的半径为9.6×106m,R=6.4×106m,地球表面重力加速度g=10m/s2.
解得:Tb=5.56h
然后再算b卫星在48小时内运行的圈数n=
=8.63圈,故选B
故答案为:5.56,B
(2)AB球碰撞过程中动量守恒,根据动量守恒定律得:
PA+PB=PA/+PB/
解得:PA/=25kgm/s
碰撞后速度相等,设此速度为v,则
mAv=25kgm/s
mBv=10kgm/s
解得:
=
碰撞前有:
mAvA=20kgm/s
mBvB=15kgm/s
解得:
=
故答案为:25,8:15
根据万有引力提供向心力得:G
| Mm |
| r2 |
| 4π2r |
| T2 |
解得:T=
|
G
| Mm |
| R2 |
而b的半径为9.6×106m,R=6.4×106m,地球表面重力加速度g=10m/s2.
解得:Tb=5.56h
然后再算b卫星在48小时内运行的圈数n=
| 48 |
| 5.56 |
故答案为:5.56,B
(2)AB球碰撞过程中动量守恒,根据动量守恒定律得:
PA+PB=PA/+PB/
解得:PA/=25kgm/s
碰撞后速度相等,设此速度为v,则
mAv=25kgm/s
mBv=10kgm/s
解得:
| mA |
| mB |
| 5 |
| 2 |
碰撞前有:
mAvA=20kgm/s
mBvB=15kgm/s
解得:
| vA |
| vB |
| 8 |
| 15 |
故答案为:25,8:15
点评:(1)利用题目提供的物理量找出不同卫星的角速度或周期关系,根据圆周运动知识求出转过的圈数.
(2)本题主要考查了动量守恒定律的直接应用,难度适中.
(2)本题主要考查了动量守恒定律的直接应用,难度适中.

练习册系列答案
相关题目
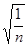 倍
倍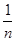 倍
倍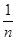 倍(忽略地球的的自转效应)
倍(忽略地球的的自转效应)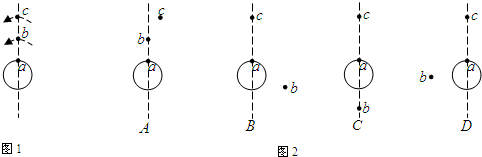
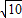 )
) 
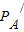 = kgm/s,碰撞前两球的速度大小之比vA:vB= .
= kgm/s,碰撞前两球的速度大小之比vA:vB= .