题目内容
两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动.现测得两星中心距离为R,其运动周期为T,求两星的总质量.
分析:双星系统中,两颗星球绕同一点做匀速圆周运动,且两者始终与圆心共线,相同时间内转过相同的角度,即角速度相等,则周期也相等.但两者做匀速圆周运动的半径不相等.
解答:解:
设两星质量分别为M1和M2,都绕连线上O点作周期为T的圆周运动,星球1和星球2到O的距离分别为l1和l2.
由万有引力定律提供向心力:
对 M1:G
=M1(
)2 l1…①
对M2:G
=M2(
)2 l2…②
由几何关系知:l1+l2=R…③
三式联立解得:M总=
.
答:两星的总质量为
设两星质量分别为M1和M2,都绕连线上O点作周期为T的圆周运动,星球1和星球2到O的距离分别为l1和l2.
由万有引力定律提供向心力:
对 M1:G
| M1M2 |
| R2 |
| 2π |
| T |
对M2:G
| M1M2 |
| R2 |
| 2π |
| T |
由几何关系知:l1+l2=R…③
三式联立解得:M总=
| 4π2R3 |
| GT2 |
答:两星的总质量为
| 4π2R3 |
| GT2 |
点评:从动力学方程的三种表述中,可得到相应的天体质量的三种表达形式:
a.M=
.
b.M=
.
c.M=
.
上述三种表达式分别对应在已知环绕天体的线速度v,角速度ω,周期T时求解中心天体质量的方法.上各式中M表示中心天体质量,m表示环绕天体质量,r表示两天体间距离,G表示万有引力常量.利用以上方法只能求出中心天体的质量,而不能求出环绕天体的质量,因为环绕天体的质量同时出现在方程的两边,已被约掉.
处理双星问题必须注意两点:(1)、两颗星球运行的角速度、周期相等;(2)、轨道半径不等于引力距离(这一点务必理解).弄清每个表达式中各字母的含义,在示意图中相应位置标出相关量,可以最大限度减少错误.
a.M=
| v2r |
| G |
b.M=
| ω2r3 |
| G |
c.M=
| 4π2r3 |
| GT2 |
上述三种表达式分别对应在已知环绕天体的线速度v,角速度ω,周期T时求解中心天体质量的方法.上各式中M表示中心天体质量,m表示环绕天体质量,r表示两天体间距离,G表示万有引力常量.利用以上方法只能求出中心天体的质量,而不能求出环绕天体的质量,因为环绕天体的质量同时出现在方程的两边,已被约掉.
处理双星问题必须注意两点:(1)、两颗星球运行的角速度、周期相等;(2)、轨道半径不等于引力距离(这一点务必理解).弄清每个表达式中各字母的含义,在示意图中相应位置标出相关量,可以最大限度减少错误.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 质量为m1、m2的两个星球组成双星,它们在相互之间的万有引力作用下绕两球连线上某点O做匀速圆周运动,则它们各自运动的周期T1:T2=
质量为m1、m2的两个星球组成双星,它们在相互之间的万有引力作用下绕两球连线上某点O做匀速圆周运动,则它们各自运动的周期T1:T2=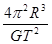 B.
B.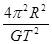 C.
C. 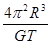 D.无法求解
D.无法求解