题目内容
如图所示,无动力传送带水平放置,传送带的质量M=5kg,长L=5m,轮与轴间的摩擦及轮的质量均不计.质量为m=2kg的工件从光滑弧面上高为h=0.45m的a点由静止开始下滑,到b点又滑上静止的传送带,工件与皮带之间的动摩擦因数 ,求:
,求:
⑴工件离开传送带时的速度;
⑵工件在传送带上运动的时间;
⑶系统损失的机械能.
 ,求:
,求:
⑴工件离开传送带时的速度;
⑵工件在传送带上运动的时间;
⑶系统损失的机械能.
(1)工件离开传送带时的速度为1m/s
(2)工件在传送带上运动的时间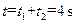
(3)系统损失的机械能等于滑动摩擦力跟工件与传送带间的相对位移的乘积,即

(2)工件在传送带上运动的时间
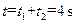
(3)系统损失的机械能等于滑动摩擦力跟工件与传送带间的相对位移的乘积,即

⑴设工件从弧面上下滑到b点时速度为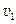 ,由机械能守恒定律得
,由机械能守恒定律得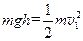
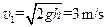 ①
①
假设工件到达传送带c端前已经与传送带速度相等,设为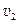 ,由于轮的质量及轮与轴间的摩擦不计,传送带可简化为放在光滑水平地面上的长木板,工件和传送带水平方向不受外力,动量守恒,有
,由于轮的质量及轮与轴间的摩擦不计,传送带可简化为放在光滑水平地面上的长木板,工件和传送带水平方向不受外力,动量守恒,有 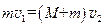
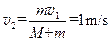 ②
②
在此期间,工件匀减速滑动的加速度为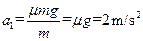 ③
③
工件的位移 ④
④
联立①②③④解得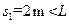 ,假设成立,即工件在到达传送带左端c之前已经与传送带速度相等,之后与传送带以速度
,假设成立,即工件在到达传送带左端c之前已经与传送带速度相等,之后与传送带以速度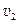 一起做匀速运动,即工件离开传送带时的速度为1m/s ⑤
一起做匀速运动,即工件离开传送带时的速度为1m/s ⑤
⑵工件在传送带上匀减速运动的时间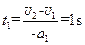 ⑥
⑥
与传送带一起匀速运动的时间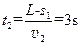 ⑦
⑦
工件在传送带上运动的时间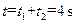 ⑧
⑧
⑶在t1时间内,传送带做匀加速运动,加速度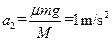 ⑨
⑨
匀加速的位移为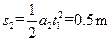 ⑩
⑩
系统损失的机械能等于滑动摩擦力跟工件与传送带间的相对位移的乘积,即
 11
11
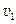 ,由机械能守恒定律得
,由机械能守恒定律得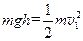
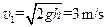 ①
①假设工件到达传送带c端前已经与传送带速度相等,设为
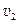 ,由于轮的质量及轮与轴间的摩擦不计,传送带可简化为放在光滑水平地面上的长木板,工件和传送带水平方向不受外力,动量守恒,有
,由于轮的质量及轮与轴间的摩擦不计,传送带可简化为放在光滑水平地面上的长木板,工件和传送带水平方向不受外力,动量守恒,有 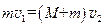
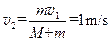 ②
②在此期间,工件匀减速滑动的加速度为
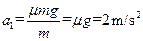 ③
③工件的位移
 ④
④联立①②③④解得
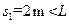 ,假设成立,即工件在到达传送带左端c之前已经与传送带速度相等,之后与传送带以速度
,假设成立,即工件在到达传送带左端c之前已经与传送带速度相等,之后与传送带以速度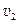 一起做匀速运动,即工件离开传送带时的速度为1m/s ⑤
一起做匀速运动,即工件离开传送带时的速度为1m/s ⑤⑵工件在传送带上匀减速运动的时间
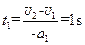 ⑥
⑥与传送带一起匀速运动的时间
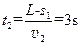 ⑦
⑦工件在传送带上运动的时间
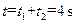 ⑧
⑧⑶在t1时间内,传送带做匀加速运动,加速度
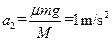 ⑨
⑨匀加速的位移为
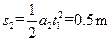 ⑩
⑩系统损失的机械能等于滑动摩擦力跟工件与传送带间的相对位移的乘积,即
 11
11
练习册系列答案
相关题目
 角,由静止开始释放摆锤,当其到达最低位置时,受到竖直挡板P阻挡而停止运动,这时铁片将作平抛运动而飞离摆锤,用刻度尺量出铁片的水平位移为s,下落高度为H.
角,由静止开始释放摆锤,当其到达最低位置时,受到竖直挡板P阻挡而停止运动,这时铁片将作平抛运动而飞离摆锤,用刻度尺量出铁片的水平位移为s,下落高度为H.


 角(
角(
 和弹力作用
和弹力作用