题目内容
 某区域内存在着电场,电场线在竖直平面内的分布如图所示,一个质量为m、电荷量为q的小球在该电场中运动,小球经过A点时的速度大小为vl,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
某区域内存在着电场,电场线在竖直平面内的分布如图所示,一个质量为m、电荷量为q的小球在该电场中运动,小球经过A点时的速度大小为vl,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )| A、若v2>vl,则电场力一定做正功 | ||||
B、A、B两点间的电势差U=
| ||||
| C、小球运动到B点时所受重力的瞬时功率P=mgv2 | ||||
D、小球由A点运动到B点,电场力做的功W=
|
分析:v2>v1时,由于重力做正功,电场力不一定做正功.由电场力做功W=qU,即可求出A、B两点间的电势差U.小球运动到B点时所受重力的瞬时功率P=mgv2sinα.由动能定理可求出电场力做功.
解答:解:
A、若v2>v1时,小球的动能增大,但由于重力做正功,电场力不一定做正功.故A错误;
B、D:小球由A点运动至B点,由动能定理得:
mgH+W=
m
-
m
得,电场力做功:W=
m
-
m
-mgH
由电场力做功W=qU得,A、B两点间的电势差:U=
(
m
-
m
-mgH).故B错误,D正确;
C、小球运动到B点时重力方向与速度方向不同,则其重力的瞬时功率P=mgv2sinα.故C错误.
故选:D.
A、若v2>v1时,小球的动能增大,但由于重力做正功,电场力不一定做正功.故A错误;
B、D:小球由A点运动至B点,由动能定理得:
mgH+W=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
得,电场力做功:W=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
由电场力做功W=qU得,A、B两点间的电势差:U=
| 1 |
| q |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
C、小球运动到B点时重力方向与速度方向不同,则其重力的瞬时功率P=mgv2sinα.故C错误.
故选:D.
点评:本题主要是动能定理的应用,动能定理反映外力对物体做的总功与动能变化的关系,要在分析受力的基础上,确定哪些力对物体做功,不能遗漏.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( ) 空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是( )
 A<
A<

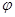 A<
A<
