题目内容
如图所示,一个质量为m的物体以某一速度从A点冲上倾角为30°的斜面,其运动的加速度大小为 ,这物体在斜面上上升的最大高度为h,则在这一过程中( )
,这物体在斜面上上升的最大高度为h,则在这一过程中( ) 
A.重力势能增加了 |
B.机械能损失了 |
| C.动能损失了mgh |
D.合外力对物体做功为 |
BD
解析试题分析:由题意知,物体在斜面上上升的最大高度为h,克服重力做功为mgh,则重力势能增加了mgh.故A错误;根据牛顿第二定律得:mgsin30°+f=ma,得到摩擦力大小为f= ,物体克服摩擦力做功为Wf=f?2h=
,物体克服摩擦力做功为Wf=f?2h= ,由功能关系知物体的机械能损失了
,由功能关系知物体的机械能损失了 ,故B正确;合力对物体做功为W合=-ma?2h=-
,故B正确;合力对物体做功为W合=-ma?2h=-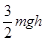 ,故D正确,又由动能定理得知,物体动能损失了
,故D正确,又由动能定理得知,物体动能损失了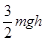 ,故C错误。
,故C错误。
考点:本题考查了功能关系 动能定理

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案如图所示,足够长的传送带以恒定速率沿顺时针方向运转.现将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段匀速运动到传送带顶端.则下列说法中正确的是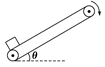
| A.第一阶段和第二阶段摩擦力对物体都做正功 |
| B.第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加量 |
| C.第二阶段摩擦力对物体做的功等于第二阶段物体机械能的增加量 |
| D.两个阶段摩擦力对物体所做的功等于物体机械能的减少量 |
质量为m的物体从距离地面h高处由静止开始加速下落,其加速度大小为 g。在物体下落过程中
g。在物体下落过程中
A.物体的动能增加了 mgh mgh |
B.物体的重力势能减少了 mgh mgh |
C.物体的机械能减少了 mgh mgh |
| D.物体的机械能保持不变 |
一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平力F的作用下,开始由平衡位置P点缓慢的移动到Q点,此时绳与竖直方向的偏角为θ,如图所示,则力F所做的功为
| A.mgLcosθ | B.FLsinθ | C.mgL(1-cosθ) | D.FL(1-cosθ) |
如图所示,实线为电场线,虚线为等势线,且相邻两条等势线间的电势差相等。一正电荷(只在电场力的作用下)在φ3上时,具有的动能是20eV,它运动到等势线φ1上时,速度为零。令φ2=0。那么该电荷的电势能为4 eV时,其动能大小为: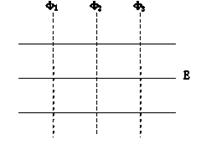
| A.16eV | B.6eV | C.10eV | D.4eV |
如图所示,幼儿园的小朋友在做滑梯游戏时,三个小朋友分别经 三条不同的路径从滑梯的顶端滑到底端.设三位小朋友的体重相同,则比较三者的下滑过程有
三条不同的路径从滑梯的顶端滑到底端.设三位小朋友的体重相同,则比较三者的下滑过程有
| A.克服摩擦力做功一定相等 |
| B.到达底端的动能一定相同 |
| C.三条不同路径重力做的功一定相等 |
D.沿路径 下滑时到达底端的动能一定最大 下滑时到达底端的动能一定最大 |
如图所示,一个小球(视为质点)从H=12 m高处,由静止开始沿光滑弯曲轨道AB,进入半径R=4 m的竖直圆环内侧,且与圆环的动摩擦因数处处相等,当到达圆环顶点C时,刚好对轨道压力为零;然后沿CB圆弧滑下,进入光滑弧形轨道BD,到达高度为h的D点时速度为零,则h的值可能为
| A.10 m | B.9.5 m | C.8.5 m | D.8 m |
如图所示,一个带负电的油滴以初速度v0从P点倾斜向上进入水平方向的匀强电场中,若油滴到达最高点C时速度大小仍为v0,则油滴最高点的位置在( )
| A.P点的左上方 | B.P点的右上方 |
| C.P点的正上方 | D.上述情况都可能 |
 的光滑绝缘斜面处于电场中,一带电量为
的光滑绝缘斜面处于电场中,一带电量为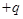 、质量为
、质量为 的小球,以初速度
的小球,以初速度 从斜面底端A点开始沿斜面上滑,当到达斜面顶端B点时,速度仍为
从斜面底端A点开始沿斜面上滑,当到达斜面顶端B点时,速度仍为

