题目内容
如图所示，质量分别为m和M的A、B两方形物块用线捆在一起，B与竖直轻弹簧相连并悬于O点，它们一起在竖直方向上做简谐运动，在振动中两物块的接触面总处在竖直位置.设弹簧的劲度系数为k，当两物块在振动中通过平衡位置时，A、B间的静摩擦力值为f0;若它们向下离开平衡位置的位移为x时，A、B间的静摩擦力值为fx,则…（ ）
A.f0=mg
B.f0=(M-m)g
C.fx=mg+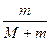
kx
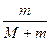D.fx=kx-mg
A.f0=mg
B.f0=(M-m)g
C.fx=mg+
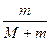kxD.fx=
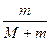kx-mgAC
当A、B一起经平衡位置时，二者受力均平衡.
对A有：f0="mg " ①
故A对，B错.
当A、B一起经平衡位置以下x处时，对整体由牛顿第二定律得：kx="(M+m)a " ②
(a方向：竖直向上)
此时对A有：fx-mg="ma " ③
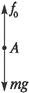由②③得fx=mg+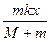
故C对D错.
对A有：f0="mg " ①
故A对，B错.
当A、B一起经平衡位置以下x处时，对整体由牛顿第二定律得：kx="(M+m)a " ②
(a方向：竖直向上)
此时对A有：fx-mg="ma " ③
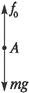由②③得fx=mg+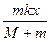故C对D错.
练习册系列答案
相关题目
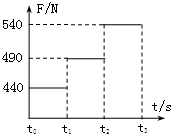
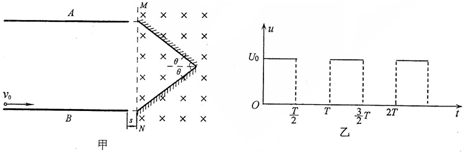
＝1.0×108C/kg，初速度v0＝2×105m/s（粒子重力不计），在A、B两板间加上如图乙所示的电压，电压的周期T＝2.0×10－6s，t＝0时刻A板电势高于B板电势，两板间电场可视为匀强电场，电势差U0＝360V，A、B板右侧相距s＝2cm处有一边界MN，在边界右侧存在一垂直纸面向里的匀强磁场，磁感应强度B＝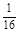
T，磁场中放置一“＞”型荧光板，位置如图所示，板与水平方向夹角θ＝37°，不考虑粒子之间相互作用及粒子二次进入磁场的可能，求：