题目内容
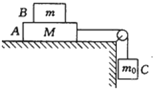
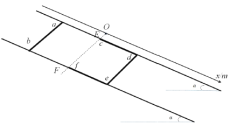
【题目】如图所示,足够长且电阻忽略不计的两平行金属导轨固定在倾角为α=30°绝缘斜面上,导轨间距为l=0.5m。沿导轨方向建立x轴,虚线EF与坐标原点O在一直线上,空间存在垂直导轨平面的磁场,磁感应强度分布为![]() (取磁感应强度B垂直斜面向上为正)。现有一质量为
(取磁感应强度B垂直斜面向上为正)。现有一质量为![]() kg,边长均为l=0.5m的U形框cdef固定在导轨平面上,c点(f点)坐标为x=0。U形框由金属棒de和两绝缘棒cd和ef组成,棒de电阻为
kg,边长均为l=0.5m的U形框cdef固定在导轨平面上,c点(f点)坐标为x=0。U形框由金属棒de和两绝缘棒cd和ef组成,棒de电阻为![]() 。另有一质量为
。另有一质量为![]() kg,长为l=0.5m,电阻为
kg,长为l=0.5m,电阻为![]() 的金属棒ab在离EF一定距离处获得一沿斜面向下的冲量I后向下运动。已知金属棒和U形框与导轨间的动摩擦因数均为
的金属棒ab在离EF一定距离处获得一沿斜面向下的冲量I后向下运动。已知金属棒和U形框与导轨间的动摩擦因数均为![]() 。
。
(1)若金属棒ab从某处释放,且I=0.4N·s,求释放瞬间金属棒ab上感应电流方向和电势差![]() ;
;
(2)若金属棒ab从某处释放,同时U形框解除固定,为使金属棒与U形框碰撞前U形框能保持静止,求冲量I大小应满足的条件。
(3)若金属棒ab在x=-0.32m处释放,且I=0.4N·s,同时U形框解除固定,之后金属棒ab运动到EF处与U形框发生完全非弹性碰撞,求金属棒cd最终静止的坐标。
【答案】(1)感应电流方向从b到a;0.1V;(2)0.48N![]() s;(3)2.5m
s;(3)2.5m
【解析】
(1)金属棒获得冲量I后,速度为
![]()
根据右手定则,感应电流方向从b到a;
切割磁感线产生的电动势为
![]()
其中![]() T;
T;
金属棒ab两端的电势差为
![]()
(2)由于ab棒向下运动时,重力沿斜面的分力与摩擦力等大反向,因此在安培力作用下运动,ab受到的安培力为
![]()
做加速度减小的减速运动;由左手定则可知,cd棒受到安培力方向沿轨道向上,大小为
![]()
其中![]() ;
;
因此获得冲量一瞬间,cd棒受到的安培力最大,最容易发生滑动
为使线框静止,此时摩擦力沿斜面向下为最大静摩擦力,大小为
![]()
因此安培力的最大值为![]() ;
;
可得最大冲量为
![]() N·s
N·s
(3)当I=0.4N·s时,金属棒获得的初速度为![]() ,其重力沿斜面分力与摩擦力刚好相等,在安培力作用下做加速度减小的减速,而U形框在碰撞前始终处于静止;
,其重力沿斜面分力与摩擦力刚好相等,在安培力作用下做加速度减小的减速,而U形框在碰撞前始终处于静止;
设到达EF时速度为![]() ,取沿斜面向下为正,由动量定理得
,取沿斜面向下为正,由动量定理得
![]()
其中![]()
解得
![]()
金属棒与U形线框发生完全非弹性碰撞,由动量守恒得
![]()
因此碰撞后U形框速度为
![]()
同理:其重力沿斜面的分力与滑动摩擦力等大反向,只受到安培力的作用,当U形框速度为v时,其感应电流为
![]()
其中,![]() ,
,![]() 分别为de边和ab边处的磁感应强度,电流方向顺时针,受到总的安培力为
分别为de边和ab边处的磁感应强度,电流方向顺时针,受到总的安培力为
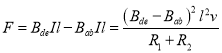
其中,![]()
由动量定理得
![]()
因此向下运动的距离为
![]()
此时cd边的坐标为
x=2.5m

 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
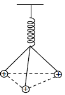
互动课堂系列答案【题目】如图所示,轻质弹簧一端系在墙上,另一端系在三根长度相同的轻绳上,轻绳的下端各系质量与电荷量均相同的带正电小球,且三个小球均处于静止状态,已知重力加速度为g。四种情形下每个小球受到的电场力大小与轻绳长度、小球质量、小球电荷量的关系如表所示,以下说法正确的是( )
情形 | 轻绳长度 | 小球质量 | 小球电荷量 | 小球受到的电场力大小 |
1 | L | m | ① |
|
2 | 2L | m | ② |
|
3 | L | 2m | ③ |
|
4 | L | m | ④ |
|
A.②中电荷量为①中电荷量的![]() 倍
倍
B.③中电荷量为②中电荷量的![]() 倍
倍
C.④中电荷量为③中电荷量的![]() 倍
倍
D.情形④下弹簧的伸长量最大
【题目】在“测定一节干电池的电动势和内阻”实验中,某小组利用图1所示电路进行测量,得到的五组数据如表所示(缺少一个电流的数值)。
(1)实验过程中滑动变阻器应___________(填“从左往右”或“从右往左”)滑动;
(2)缺少的电流数值如图2所示,则电流表的读数应为___________A;

(3)据上述五组数据画出的U-I图像如图3所示,求得干电池的内阻为___________Ω(保留2位有效数字),若考虑流过电压表的电流,电动势的真实值应___________(填“略大于”或“略小于”)电动势的测量值。
实验次数 | 1 | 2 | 3 | 4 | 5 |
电流I/A | 0.10 | 0.20 | 0.40 | 0.50 | |
电压U/V | 1.37 | 1.29 | 1.20 | 1.12 | 1.05 |